Diferencia entre revisiones de «Semigrupo conmutativo»
(→Fuentes) |
(Deshecha la edición 1705305 de Yoandrys.aduana hlg (disc.)) |
||
| Línea 49: | Línea 49: | ||
==Fuentes== | ==Fuentes== | ||
| − | + | # Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967. | |
| − | + | </div> | |
[[Categoría:Campos,_anillos,_álgebras]][[Categoría:Álgebra]][[Categoría:Matemáticas]] | [[Categoría:Campos,_anillos,_álgebras]][[Categoría:Álgebra]][[Categoría:Matemáticas]] | ||
Revisión del 09:00 26 oct 2012
| ||||||
Semigrupo conmutativo o abeliano. En Álgebra dícese de la estructura algebraica conformada por el par <G,*>, tales que G es un conjunto no vacío y * es una operación binaria; entonces se cumple que * es cerrada, asociativa y conmutativa.
Definición
Sea un conjunto G y la operación binaria * definida como *(x,y)=z, normalmente escrita como x*y=z que satisface los axiomas:
- Clausura:
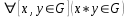 . * es cerrada.
. * es cerrada. - Asociatividad: Para todo x, y, z de G, (x*y)*z=x*(y*z).
- Conmutatividad: Para todo x, y de G, x*y=y*x.
Se dice que G con la operación * es un semigrupo conmutativo o abeliano.
En otras palabras, un semigrupo abeliano es un semigrupo cuya operación también es conmutativa.
Ejemplos
- Todo grupo conmutativo <G,*> es un semigrupo conmutativo.
- Los siguientes son semigrupos abelianos representados en forma tabular:
| <{a,b},@> | <{a,b,c},*> | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
- Es un semigrupo conmutativo las matrices complejas
 con la operación suma de matrices definidas de la manera tradicional:
con la operación suma de matrices definidas de la manera tradicional:
Fuentes
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.

