Anillo (álgebra)

Anillo algebraico Concepto: Estructura algebraica de un conjunto no vacío y dos operaciones *, @ sobre éste cerradas y asociativas, * es conmutativa y en ella se verifica la existencia del neutro y los inversos para cada elemento del conjunto y juntas * y @ satisfacen la distributividad.

Anillo . En Álgebra dícese del estructura algebraica conformada por la terna <A,*,@>, donde A es un conjunto no vacío, * y @ son operaciones binarias; y se cumple estrictamente que * es cerrada, asociativa y conmutativa, sobre ella existe el elemento neutro y también los inversos de cada elemento de A. @ es cerrada y asociativa.@ es distributiva respecto a la operación * :Esto es: a@(b *c) = (a @ b) * (a @ c).

En el caso que <A,*,@> sea un anillo y @ sea conmutativa se dice que es un anillo conmutativo. Además, si existe el neutro sobre @ llamado elemento unidad se dice que <A,*,@> es un anillo conmutativo con elemento unidad.

Si <A,*,@> es un anillo y existe el elemento unidad para @ se está en presencia de un anillo con elemento unidad.

Definición

Sea un conjunto A no vacío y las operaciones binarias * y @ que satisfacen los siguientes axiomas:

1. Clausura de *: . * es cerrada.
2. Asociatividad de *: Para todos x, y, z de A, (x*y)*z=x*(y*z).
3. Conmutitividad de *: Para todos x e y en A se cumple x*y=y*x.
4. Existencia del neutro: Existe uno y solo un elemento e de A tal que para todo x de A se cumple que x*e=e*x=x. e es llamado neutro para * en A.
5. Existencia de los inversos: Para todo x en A, existe un único elemento x" también en A, que satisface x*x"=x"*x=e. A x" se denomina inverso de x según *.
6. Clausura de @: 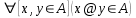. * es cerrada.
7. Asociatividad de @*: Para todos x, y, z de A, (x@y)@z=x@(y@z).
8. Distributividad: Para todos x, y, z de A, x@(y*z)=x@y * x@z.

Se dice que A con las operaciones * y @ es un anillo.

El incumplimiento de cualquiera de los axiomas precedentes inhabilita la condición de anillo.

Apoyándose en otras definiciones del álgebra puede decirse que:

• Sea A un conjunto no vacío con dos operaciones binarias * y @ es un anillo si y sólo si <A,*> es un grupo abeliano, <A,@> es un monoide y se satisface la ley distributiva x@(y*z)=(x@y)*(x@z) para todos x, y, z de A

Definición alternativa

Un conjunto S se denomina anillo, si se han definido sobre él dos operaciones , denominadas adición y multiplicación, siendo ambas conmutativas y asociativas, y vinculadas por la ley distributiva, conllevando además la adición la operación inversa, denominada resta.

Ejemplos

1. Los números enteros son un anillo de la forma .
2. Sea M_n el conjunto de las matrices cuadradas de orden n, puede decirse que 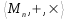es un anillo.
   1. Para todas las matrices cuadradas de n filas A y B A+B también es una matriz cuadrada de n filas y columnas.
   2. La suma de matrices cuadradas del mismo orden n es asociativa.
   3. La suma de matrices cuadradas del mismo orden n es conmutativa.
   4. es el neutro para la suma.
   5. Para toda matriz cuadrada de n filas y columnas se tiene su inverso dado por y según la suma de matrices .
   6. El producto de matrices cuadradas de orden n es cerrado.
   7. El producto de matrices cuadradas de orden n es asociativo.
   8. Para todas matrices cuadradas de orden n A, B, C se cumple A(B+C)=AB+AC.
3. Todo cuerpo <C,*,@> es también un anillo.
4. Por tanto los conjuntos numéricos racionales, reales y complejos que son cuerpos con la suma y la multiplicación también se constituyen en anillos sobre esas mismas operaciones.

Fuentes

• Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.

A.G. Kurosch. Curso de álgebra superior. Editorial Mir, Moscú (1981) Impreso en la URSS. Traducido del ruso por Emiliano APARICIO BERNARDO