Grupo algebraico

Grupo Concepto: Estructura algebraica de un conjunto y una operación sobre éste que es cerrada y asociativa, además de que existe un neutro en el conjunto para la operación e inversos.

Grupo algebraico. En Álgebra dícese de la estructura algebraica conformada por el par <G,*>, tales que G es un conjunto no vacío y * es una operación binaria; entonces se cumple que * es cerrada y asociativa y que existe el elemento neutro en G y también los inversos según * de cada elemento del conjunto e cuestión.

En el caso que <G,*> sea grupo y la operación sea conmutativa se dice que es un grupo conmutativo o abeliano.

El concepto de grupo se debe al célebre matemático francés Évariste Galois, muerto en duelo a los 21 años.

Definición

Sea un conjunto G y la operación binaria * definida como *(x,y)=z y se satisfacen los siguientes axiomas:

1. Clausura: 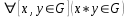. * es cerrada.
2. Asociatividad: Para todo x, y, z de G, (x*y)*z=x*(y*z).
3. Existencia del neutro: Existe uno y solo un elemento e de G tal que para todo x de G se cumple que x*e=e*x=x. e es llamado neutro para * en G.
4. Existencia de los inversos: Para todo x en G, existe un único elemento x" también en G, que satisface x*x"=x"*x=e. A x" se denomina inverso de x según *.

Se dice que G con la operación * es un grupo.

El incumplimiento de cualquiera de los axiomas precedentes inhabilita la condición de grupo.

Ejemplos.

1. Los números enteros y la suma conforman un grupo pues la suma es cerrada y asociativa, el 0 es el neutro y para toda k entera su opuesto -k es el inverso.
2. En cambio los enteros y el producto no es un grupo pues no existe del inverso para cada elemento.
3. Sea M_n el conjunto de las matrices cuadradas de orden n, puede decirse que <M_n,+> es un grupo.
   1. Para todas las matrices cuadradas de n filas A y B A+B también es una matriz cuadrada de n filas y columnas.
   2. La suma de matrices cuadradas del mismo orden n es asociativa.
   3. es el neutro para la suma.
   4. Para toda matriz cuadrada de n filas y columnas se tiene su inverso dado por y según la suma de matrices .
4. También es un grupo <M_n,m,+>, donde M_n,m es el conjunto de matrices de n filas y m columnas.
5. Sea un cuerpo <C,*,@>; <C,*> y <C,@> son grupos.
6. El conjunto de de todas las raíces cuartas de 1, {1, -1, i, -i} con la multiplicación en C, es un grupo finito. Elemento identidad es 1; inverso de 1, -1; inverso de i, -1 y recíprocamente. Es isomorfo con el grupo aditivo de los restos de división módulo 4, {0, 1, 2, y 3} elemento identidad 0; inverso de 2, 2; inverso de 1,3 y recíprocamente.

Fuentes

• Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
• Kostrikin, A.I.. Introducción al álgebra, , traduce del ruso: Aníbal Sala Editorial MIR, Moscú, 1983 impreso en la URSS.
• Kurosch. Curso de álgebra superior, traduce del ruso Emiliano Aparicio Bernardo; Editorial Mir, Moscú, 1981 cuarta edición, impreso en la URSS.
• Birkhoff y Mac Lane. Älgebra Moderna, traduce del inglés: Rafael Rodríguez Vidal; Editorial Teide, Barcelona, reimpresión 1960.
• Alexandrooff, P.S. Introducción a la teoría de grupos; traduce del ruso: Juana Elisa Quastler; Editorial Universitaria de Buenos Aires, segunda edición octubre de 1957. 1º. edición en ruso 1938, dirigido a estudios preuniversitarios y docentes de secundaria.