Diferencia entre revisiones de «Subgrupo»
m (Texto reemplazado: «<div align="justify">» por «») |
m (motivación del tema) |
||
| Línea 1: | Línea 1: | ||
{{Definición|nombre=Subgrupo|imagen=Matemática.jpg|concepto=Sea ''<G,*>'' un [[Grupo algebraico|grupo]], se llama subgrupo a cualquier [[subconjunto]] no vacío ''G' '' de ''G'' que para la misma operación ''*'', ''<G',*>'' sea un grupo también.}} | {{Definición|nombre=Subgrupo|imagen=Matemática.jpg|concepto=Sea ''<G,*>'' un [[Grupo algebraico|grupo]], se llama subgrupo a cualquier [[subconjunto]] no vacío ''G' '' de ''G'' que para la misma operación ''*'', ''<G',*>'' sea un grupo también.}} | ||
| − | '''Subgrupo'''. En [[Álgebra]] dícese de la [[estructura algebraica]] conformada por el par ''<G',*>'', tales que ''G' '' es un [[subconjunto]] no vacío de ''G'' y ''*'' es una [[operación binaria]] y ''<G,*>'' es un [[Grupo algebraico|grupo]] y se cumple que ''<G',*>'' es también un grupo. | + | '''Subgrupo'''. En el caso de los números enteros sabemos que constituyen un grupo algebraico con la adición usual.El conjunto Z de los enteros tiene varios subconjuntos, los más conocidos los pares, impares, primos. El objetivo apunta a saber cuáles asumen la estructura de grupo algebraico. De los mencionados sólo los pares con la adición; los impares no, fallan en la propiedad clausurativa, tan igual que los primos. Sin embargo, hay una infinidad de subconjuntos de Z que son grupos algebraicos, cualquier conjunto de todos los múltiplos de un entero fijo mayor que 1, aditivamente forman un grupo. |
| + | |||
| + | En [[Álgebra]] dícese de la [[estructura algebraica]] conformada por el par ''<G',*>'', tales que ''G' '' es un [[subconjunto]] no vacío de ''G'' y ''*'' es una [[operación binaria]] y ''<G,*>'' es un [[Grupo algebraico|grupo]] y se cumple que ''<G',*>'' es también un grupo. | ||
En el caso que ''<G',*>'' sea subgrupo y la operación sea [[Conmutatividad|conmutativa]] dentro de ''G' '' se está en presencia de un [[subgrupo conmutativo]] o ''abeliano''. | En el caso que ''<G',*>'' sea subgrupo y la operación sea [[Conmutatividad|conmutativa]] dentro de ''G' '' se está en presencia de un [[subgrupo conmutativo]] o ''abeliano''. | ||
Revisión del 11:40 1 oct 2019
| ||||||
Subgrupo. En el caso de los números enteros sabemos que constituyen un grupo algebraico con la adición usual.El conjunto Z de los enteros tiene varios subconjuntos, los más conocidos los pares, impares, primos. El objetivo apunta a saber cuáles asumen la estructura de grupo algebraico. De los mencionados sólo los pares con la adición; los impares no, fallan en la propiedad clausurativa, tan igual que los primos. Sin embargo, hay una infinidad de subconjuntos de Z que son grupos algebraicos, cualquier conjunto de todos los múltiplos de un entero fijo mayor que 1, aditivamente forman un grupo.
En Álgebra dícese de la estructura algebraica conformada por el par <G',*>, tales que G' es un subconjunto no vacío de G y * es una operación binaria y <G,*> es un grupo y se cumple que <G',*> es también un grupo.
En el caso que <G',*> sea subgrupo y la operación sea conmutativa dentro de G' se está en presencia de un subgrupo conmutativo o abeliano.
Definición.
- Sea un conjunto G y la operación binaria * un grupo algebraico <G,*>, se le llama subgrupo a cualquier
 con
con 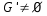 que satisfaga el hecho de ser también un grupo sobre la misma operación *.
que satisfaga el hecho de ser también un grupo sobre la misma operación *.
Una consecuencia de importancia en los subgrupos es la siguiente:
- En todo subgrupo <G',*> de <G,*> se cumple Archivo:E pertenece G prima.gif donde e es el neutro de <G,*>.
A ese subgrupo se le nombra subgrupo trivial de G para la operación * y se considera la demostración de que todo grupo tiene al menos un subgrupo.
Ejemplos.
Ejemplo 1.
El menor de los subgrupos del grupo <G,*> es <{e},*> donde e es el elemento neutro para * en G, es decir el subgrupo trivial.
Ejemplo 2.
Sea el grupo <{0;1;2;3;4},+5> cuya operación +5 (suma módulo 5) viene definida por la tabla:
| +5 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
no tiene otro subgrupo que el trivial, porque para el resto de los subconjuntos de G se incumple el axioma del cierre de los grupos.
Ejemplo 3.
Sea el grupo <{e,a,b,c},@> (Grupo Cuarto de Klein) con @ definida según la tabla siguiente:
| @ | e | a | b | c |
|---|---|---|---|---|
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
tiene a <{e},@>, <{e,a},@>, <{e,a,b},@> por subgrupo.
Fuentes
- Subgrupo
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
