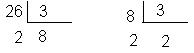Divisibilidad
| ||||||
Divisibilidad. Estudia las condiciones necesarias y suficientes para que un número sea divisible por el otro. Un número a distinto de 0 es divisor de otro número b, cuando el resto de dividir b entre a es cero, en otras palabras, cuando la división de b entre a es exacta.
Nomenclatura
Los números desde el punto de vista de su divisibilidad, pueden ser simples o primos y compuestos:
Número simple o primo: es el que solo es divisible por sí mismo y por la unidad. Ejemplo: 3; 5; 7; 23; etc.
Número compuesto: es el que además de ser divisible por sí mismo y por la unidad, es divisible también por algún otro número. Ejemplo: 6; 12; 24; etc.
Principios fundamentales
Los principios fundamentales de la divisibilidad son ciertas propiedades que sirven de base para deducir para reunir las condiciones que debe reunir un número para ser divisible por otro.
I. Si un número divide a otros varios, divide a su suma.
Ejemplo: Investigar, sin hallarla si la suma de 6; 12 y 15 será divisible por 3 .
Como 3 divide a 6, a 12, y a 15, podemos afirmar también que la suma de estos tres números será divisible por 3, aún sin saber a cuanto es igual la suma.
Respuesta: La suma será divisible por 3 por serlo 6; 12 y 15.
Prueba: 6 + 12 + 15 = 33
33: 3 = 11 Comprobando
II. Si un número divide a otros dos, divide a su diferencia.
Ejemplo: Averiguar si la diferencia entre 39 y 15 será divisible por 3 sin efectuar la resta.
Como 39 y 15 son múltiplos de 3 podemos asegurar que su diferencia también será múltiplo de 3.
Respuesta: Por ser 39 y 15 divisibles por 3, su diferencia también lo será.
III. Si un número divide a otro, divide a cualquier múltiplo de este.
Ejemplo: Investigar, sin efectuar la multiplicación, si 14 . 4 será divisible por 7
Como que 7 divide a 14 podemos asegurar que el producto de multiplicar 14 por 4 será también divisible por 7.
Respuesta: El producto será divisible por 7 por serlo 14.
Prueba: 14 . 4 = 56
56: 7 = 8 Comprobando.
IV. Si los sumandos no son divisibles por un número la suma, sin embargo, podrá serlo de acuerdo a lo siguiente:
Si al dividir números dados entre otro número las divisiones no exactas, pero la suma de los restos de estas divisiones es divisible exactamente por ese otro número, la suma de los números dados será también divisible por él.
Ejemplo: Investigar si la suma de 23, 53 y 15 será divisible por 7, sin efectuar la división. Dividimos cada uno de estos números por 7 para hallar los restos.
Y como la suma de los restos 2 + 4 + 1 = 7, la suma de los números 23; 53 y 15 será también múltiplo de 7, con toda seguridad. Respuesta: La suma de 23, 53 y 15 será divisible por 7 por serlo la suma de los restos obtenidos al dividir por 7 dichos números.
Prueba: 23 + 53 + 15 = 91
91 : 7 = 13 Comprobando.
V. Si al dividir dos números dados entre un tercero las divisiones no son exactas, pero los resto de esas divisiones son iguales, la diferencia de estos números será divisible por el tercero.
Ejemplo: Averiguar sin, sin efectuar la resta, si la diferencia entre 26 y 8 será divisible por 3.
Como los restos son iguales, 2 = 2, podemos afirmar que la diferencia entre 26 y 8 será divisible por 3.
Respuesta: Como al dividir 26 y 8 por 3 los restos son iguales, la diferencia de 26 y 8 será divisible por 3.
Prueba: 26 – 8 = 18
18 : 3 = 6 comprobando.
VI. Si un número divide al dividendo y al divisor, divide al resto.
Ejemplo: Como 7 divide a 21 y a 35, el resto de 35 : 21 tiene que ser divisible por 7. En efecto:
El resto es 14 que es múltiplo de 7.
VII. Si un número divide al divisor y al resto, divide también al dividendo.
En efecto, al dividir al divisor divide también al producto del divisor por el cociente de acuerdo con el tercer principio.
Véase también
Fuentes
- Sócrates Rosell, F. Volumen I(Segunda Edición). Editorial Pedagógica.