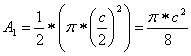Teorema de Pitágoras

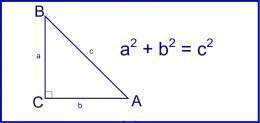
Teorema de Pitágoras Concepto: En todo triángulo rectángulo el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos.

Teorema de Pitágoras. Proposición que compara los tres lados de un triángulo rectángulo, y establece que el cuadrado de la longitud c de la hipotenusa AB es igual a la suma de los cuadrados de las respectivas longitudes a y b de sus catetos CB y CA: c² = a² + b²

Historia

El Teorema de Pitágoras fue descubierto aproximadamente en el año 500 a.n.e y lleva este nombre porque su descubrimiento recae sobre la escuela pitagórica. Si bien los pitagóricos no descubrieron este teorema (ya era conocido y aplicado en Babilonia y la India desde hacía un tiempo considerable), sí fueron los primeros en encontrar una demostración formal del teorema. También demostraron el converso del teorema (si los lados de un triángulo satisfacen la ecuación, entonces el triángulo es recto).

Aplicaciones

El teorema de Pitágoras tiene numerosas aplicaciones, como el cálculo de la medida de los lados de un triángulo o de magnitudes en otros polígonos.

Conociendo la hipotenusa y un cateto, calcular el otro cateto

A partir de la expresión general del teorema de Pitágoras, despejamos los catetos a y b: Si c2=a2+b2 tenemos que

y

Reconocimiento de triángulos rectángulos.

Un triángulo es rectángulo si sus lados verifican la relación del teorema de Pitágoras. Si c² ≠ a² + b², entonces puede ocurrir que:

• c² > a² + b², el área del cuadrado sobre la hipotenusa es mayor que la suma de las áreas de los cuadrados construidos sobre los catetos. El triángulo es obtusángulo.
• c² < a² + b², el área del cuadrado sobre la hipotenusa es menor que la suma de las áreas de los cuadrados construidos sobre los catetos. El triángulo es acutángulo.

Aplicaciones en Geometría

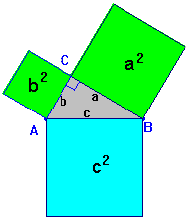
Geométricamente, el teorema de Pitágoras quiere decir que si dibujamos tres cuadrados, de forma que cada uno tenga el lado igual a uno de los tres lados de un triángulo rectángulo, se cumple que el área del cuadrado mayor es igual a la suma de las áreas de los otros dos.

Comprensión del teorema

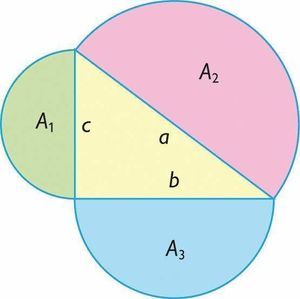
Ahora bien, ¿esto ocurre solamente si la figura que dibujamos es un cuadrado o pasa también con otras? En concreto, si tenemos un triángulo rectángulo y dibujamos tres semicírculos cuyos diámetros son los tres lados del triángulo, ¿hay alguna relación entre las áreas de esos semicírculos?

Demostración del teorema

El radio de cada uno de los semicírculos es la mitad del lado correspondiente, por lo que sus áreas son:

y de igual forma:

y

Sumando las áreas:

puesto que al ser el triángulo rectángulo se cumple que c²=a²+b²

Luego se verifica la igualdad de áreas con semicírculos.

Demostraciones

El Teorema de Pitágoras es de los que cuentan con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Las demostraciones están divididas en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo; geométricas, en las que se realizan comparaciones de áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.

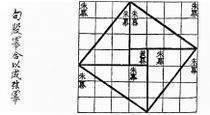
El Chou Pei Suan Ching

Prueba visual para un triángulo de a = 3, b = 4 y c = 5 como se ve en el Chou Pei Suan Ching, 500-200 a.n.e.

El Chou Pei es una obra matemática que se considera mayoritariamente fue escrita entre el 500 y el 300 a.n.e. Se cree que Pitágoras no conoció esta obra. El Chou Pei demuestra el teorema construyendo un cuadrado de lado (a+b) que se parte en cuatro triángulos de base a y altura b, y un cuadrado de lado c.

Demostración

Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir: a² + b² = c² Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera: (a-b)² = a² - 2ab + b² Ya que (b-a)² = (a-b)² Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor: c² = 4 *( a * b/2) + a² - 2ab + b²= a² + b² y así ha quedando demostrado el teorema.

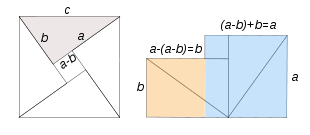
Demostración de Bhaskara

Bhaskara desarrolla una demostración gráfica y algebraica del teorema de Pitágoras.

Bhaskara II, matemático y astrónomo hindú del siglo XII, da la siguiente demostración del teorema de Pitágoras. Con cuatro triángulos rectángulos de lados a, b y c se construye el cuadrado de lado c –izquierda-, en cuyo centro se forma otro cuadrado de lado (a-b). Redistribuyendo los cuatro triángulos y el cuadrado de lado (a-b), construimos la figura de la derecha, cuya superficie resulta ser la suma de la de dos cuadrados: uno de lado a –azul- y otro de lado b -naranja-. Se ha demostrado gráficamente que c²=a²+b² Algebraicamente: el área del cuadrado de lado c es la correspondiente a los cuatro triángulos, más el área del cuadrado central de lado (a-b), es decir: c²=4 * ab/2+ (a-b) ² expresión que desarrollada y simplificada da el resultado c²=a²+b², y el teorema queda demostrado.

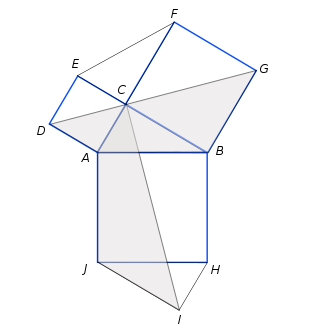
Demostración de Leonardo da Vinci

El diseño inicial, con el triángulo y los cuadrados de catetos e hipotenusa, es modificado por Leonardo da Vinci al añadir dos triángulos iguales al ABC: el ECF y el HIJ.

El teorema de Pitágoras también fue abordado por una personalidad del Renacimiento, Leonardo da Vinci. Partiendo del triángulo rectángulo ABC con los cuadrados de catetos e hipotenusa, Leonardo añade los triángulos ECF y HIJ, iguales al dado, resultando dos polígonos, cuyas superficies va a demostrar que son equivalentes:

1. Polígono ADEFGB: la línea DG lo divide en dos mitades idénticas, ADGB y DEFG.
2. Polígono ACBHIJ: la línea CI determina CBHI y CIJA.

Comparando los polígonos destacados en gris, ADGB y CIJA:

• Se aprecia de inmediato que tienen tres lados iguales: AD=AC, AB=AJ, BG=BC=IJ
• Asimismo es inmediata la igualdad entre los ángulos de los siguientes vértices:
  • A de ADGB y A de CIJA
  • B de ADGB y J de CIJA

Se concluye que ADGB y CIJA son iguales. De modo análogo se comprueba la igualdad entre ADGB y CBHI. Además, un giro de centro A, y sentido positivo, transforma CIJA en ADGB. Mientras que un giro de centro B, y sentido negativo, transforma CBHI en ADGB. Todo ello permite establecer que los polígonos ADEFGB y ACBHIJ tienen áreas equivalentes. Si a cada uno se le quita sus dos triángulos –iguales- las superficies que restan forzosamente serán iguales. Y esas superficies no son sino los dos cuadrados de los catetos en el polígono ADEFGB, por una parte, y el cuadrado de la hipotenusa en el polígono ACBHIJ, por la otra. El teorema de Pitágoras queda demostrado.

Prueba usando la ley de los cosenos

Se puede demostrar por la ley de los cosenos

Se tiene que c² = a² +b² - 2ab cos C.

En la expresión anterior cuando C → 90º , cosC → 0, por tanto

resulta que c² = a² +b²

Prueba usando la ley de cosenos

Se puede demostrar por la ley de los cosenos

Se tiene que c² = a² +b² - 2ab cos C.

En la expresión anterior cuando C → 90º , cosC → 0, por tanto

resulta que c² = a² +b²

Usos en la práctica social

• Para hallar la longitud de una escalera conociendo la altura del punto de la pared donde se recuesta, la separación desde la línea muro piso hasta el pie de la escalera.
• Calcular el diámetro de una tapa circular, se coloca una escuadra informal, cuyo vértice toca un punto del borde; se miden las sendas distancias del vértice a los puntos del borde donde la escuadra los interseca. Aplicando el teorema de Pitágoras, con las distancias anteriores se obtiene el diámetro.
• Construir una vereda diagonal. Para ello calcular la diagonal, no accesible, de un terreno rectangular o cuadrado, pero sí dos lados del terreno concurrentes pueden ser medidos.
• En tres dimensiones, para hallar la longitud de la diagonal de una esquina suelo dos muros, hasta la esquina opuesta de bóveda con dos muros. Si se trata de salón de clase se debe medir previamente: el ancho, largo y altura.

Aplicación empírica

• Un almacén, con forma de cuadrado de lado 13 metros, otros dos de forma cuadrada y lados de 5 y 12 metros respectivamente, tienen la misma altura de 3 metros; por lo tanto: sus volúmenes cumplen:

3x13² = 3x 5² + 3x 12², esto es 505 = 75 + 432

una variación del Teorema de Pitágoras, pues la terna ordenada (5,12,13) es pitagórica.

• Además si guardamos arena en estos almacenes, el peso de la arena en el almacén más extenso, será igual a la suma de los pesos de la arena guardada en los almacenes de menor lado. Sabemos que peso = volumen por peso específico. En el caso anterior, el peso específico de la arena es 1.6Tm/m³. De donde:

507x 1.6 = 75x 1.6 +432x1.6, luego 811.2 = 120 +432x1.6

Ver también

• Triángulo
  
• Geometría
  
• Cuadrado.
  
• Rectángulo.
  
• Círculo.
  
• Paralelogramo.
  
• Cuadrilátero.
  

Fuentes

• Geometría en Kalipedia.com Consultado 30 septiembre de 2010
• Microsoft ® Encarta ® 2007. © 1993--2006 Microsoft Corporation. Reservados todos los derechos.
• TEOREMA DE PITÁGORAS Consultado 30 septiembre de 2010
• Teorema de Pitágoras - Wikipedia Consultado 1 octubre de 2010