Al-Juarismi
| ||||||||||||
Al-Jwarizmi. Célebre matemático árabe de la primera mitad del siglo IX. De su nombre y de sus obras proceden las palabras «álgebra», «guarismo» y «algoritmo». Gracias a él, se introdujo en Occidente el actual sistema de numeración.
Sumario
Síntesis biográfica
Nació en Jiva (Uzbekistán), 700 km al noroeste de la ciudad de Samarcanda (Uzbekistán), y 2500 km al noreste de Bagdad.
Su nombre completo era Abu Jafar Muhammad ibn Musa Al-Jwarizmi, que en árabe significa ‘Mohamed, hijo de Moisés, padre de Jafar, el de Corasmia’. El hecho de que en su nombre completo se mencione el lugar de nacimiento significa que era un hombre famoso. Khwarizm, actualmente Khiva, es una ciudad que se encuentra al sudeste del mar de Aral, en Uzbekistán, territorio por el que pasaba la antigua ruta de la seda y que había sido conquistado por los árabes en el siglo VIII.
La fecha de nacimiento de Al-Jwarizmi se calcula entre los años 780 y 800.
Trayectoria
Trabajó en la ciudad persa de Bagdad en la primera mitad del siglo IX, en la corte del califa Al-Mamun, quien fundó la casa de la sabiduría (Bayt al-Hikma), lugar destinado al desarrollo de las ciencias que muchos han comparado con la Biblioteca de Alejandría.
En este lugar se desempeñó entre otras cosas como bibliotecario. Participa activamente en la primera expedición realizada por los árabes para medir la circunferencia de la Tierra.
Otro punto no esclarecido en la biografía de este sabio es si ya estaba familiarizado con los trabajos de [Euclides]], para Gandz estos trabajos le eran desconocidos, no obstante hay que tener en cuenta que Abu Abdallah fue compañero de Al-Hajjaj en la Casa de la Sabiduría, y este último durante el reinado de Harun al-Rashid había traducido al árabe el libro Los elementos, de Euclides.
-
-
-
Síntesis biográfica
Reinaba el califa Harun al-Rashid, quinto califa de la dinastía Abbasid. La capital estaba en Bagdag. Harun, tuvo dos hijos y a su muerte, hubo una guerra de sucesión entre los dos hermanos, al-Amin y al-Mamun. Ganó la guerra al-Mamun y al-Amin fue ejecutado en 813.
Al-Mamun continuó el patronazgo de las artes y la cultura que había iniciado su padre y fundó la Casa de la Sabiduría, donde enseñaban filósofos y científicos griegos. También construyó una biblioteca y un observatorio astronómico.
Al-Khwarizmi fue bibliotecario en la corte del califa al-Mamun y astrónomo en el observatorio de Bagdad. Sus trabajos de álgebra, aritmética y tablas astronómicas adelantaron enormemente el pensamiento matemático.
Fallecimiento
Falleció en Bagdad hacia el año 846, 848 u 850.
Obra
La obra Al-jebr w'al-muqabalah fue traducida al latín, por primera vez, en la Escuela de Traductores de Toledo (España) y tuvo mucha influencia en las matemáticas de la época. La traducción del título de la obra era complicado, por lo que los traductores optaron por latinizar el título, convirtiéndolo en «aljeber» que acabó derivando en el actual álgebra.
La versión latina del tratado de al-Khwarizmi sobre álgebra fue responsable de gran parte del conocimiento matemático en la Europa medieval.
En España, donde la influencia árabe fue muy importante, surgió el término «álgebra», se utilizó para referirse al arte de restituir a su lugar los huesos dislocados y el término algebrista que era la persona que sabía arreglar las dislocaciones.
Otro libro de al-Kharizmi fue De numero indiorum (‘sobre los números hindúes’). En este libro se dan las reglas para hacer las operaciones aritméticas. Estas reglas se denominaron como las reglas de al-Kharizmi y por deformación de la palabra llegó al término actual «algoritmo».
Su trabajo con los algoritmos introdujo el método de cálculo con la utilización de la numeración arábiga y la notación decimal. Las matemáticas le deben a al-Khwarizmi la introducción del sistema de numeración actual y el álgebra.
La mayoría de sus diez obras son conocidas en forma indirecta o por traducciones hechas más tarde al latín (muchas de ellas en Toledo) y de algunas solo se conoce el título.
Al-Khwarizmi fue un recopilador del conocimiento de los griegos e hindúes, principalmente de matemáticas, pero también de astronomía (incluyendo el calendario judío), astrología, geografía e historia.
Su trabajo más conocido y usado fueron sus Tablas Astronómicas, basadas en conocimientos de los indios. Incluyen algoritmos para calcular fechas y las primeras tablas conocidas de las funciones trigonométricas ―seno y cotangente―, las que posteriormente fueron corregidas por el astrónomo Mostema-ben Ahmed el Magerit y su hija Fátima de Madrid.
Aritmética
De su aritmética, posiblemente denominada originalmente Kitab al-Jam'a wal-Tafreeq bil Hisab al-Hindi, solo conservamos la versión latina, Algoritmi de número indorum, del siglo XII. En esta obra describe con detalle el sistema indio de numeración posicional en base 10 y la manera de para hacer cálculos con él. Se sabe que en la versión árabe había un método para hallar raíces cuadradas, pero este método no aparece en la versión latina. Fue esencial para la introducción de este sistema de numeración en el mundo árabe y posteriormente en Europa. El que nos haya llegado a través de los árabes hace que le llamemos habitualmente sistema de numeración árabe, cuando deberíamos llamarlo indo-arábigo. Posiblemente fuese el primero en utilizar el cero como una cifra.
Tratado de Álgebra
Su tratado de álgebra es una introducción compacta al cálculo, usando reglas para completar y reducir ecuaciones. Además de sistematizar la resolución de ecuaciones cuadráticas, también trata geometría, cálculos comerciales y de herencias. Quizás éste es el libro árabe más antiguo conocido y parte de su título "Kitab al-jabr wa'l-muqabala" da origen a la palabra álgebra. Los términos al-jabr y al-muqabala se utilizan para denominar lo que nosotros entendemos por transposición de términos y posterior simplificación de términos semejantes con coeficientes negativos y positivos. Una posible traducción del título sería "El libro de restaurar e igualar" o "El arte de resolver ecuaciones".
La palabra algebrista se utiliza también en El Quijote con un significado ya en desuso, pero que hace referencia a ese significado de restauración o recomposición. En el diccionario de la Real Academia Española de la Lengua podemos leer:
Tratado sobre Astronomía
De su tratado sobre Astronomía, Sinshind zij, también se han perdido las dos versiones que escribió en árabe. Como ocurre con la aritmética, conservamos dos versiones latinas del siglo X. Incluye estudios de calendarios, posiciones reales del sol, la luna y los planetas, tablas de senos y tangentes, astronomía esférica, tablas astrológicas, cálculos de paralaje y eclipses, y visibilidad de la luna.
Geografía
En Geografía, con una obra denominada Kitab Surat-al-Ard, revisó y corrigió a Ptolomeo en lo referente a África y al Oriente. Lista latitudes y longitudes de ciudades, montañas, mares, islas, regiones geográficas y ríos, como base para un mapa del mundo entonces conocido. En este mapa dice que trabajaron a sus órdenes setenta geógrafos.
El trabajo de Al'Khwarizmi permitió preservar y difundir el conocimiento de los griegos (con la notable excepción del trabajo de Diofanto) e hindúes, pilares de nuestra civilización. Rescató de los griegos la rigurosidad y de los hindúes la simplicidad (en vez de una larga demostración, usar un diagrama junto a la palabra Mira). Sus libros son intuitivos y prácticos y su principal contribución fue simplificar las matemáticas a un nivel entendible por los no expertos. En particular, muestra las ventajas de usar el sistema posicional hindú, un atrevimiento para su época, dado lo tradicional de la cultura árabe. La exposición clara de cómo calcular de una manera sistemática por medio de algoritmos diseñados para ser usados con algún tipo de dispositivo mecánico similar a un ábaco, más que con lápiz y papel, muestra la intuición y el poder de abstracción de Al'Khwarizmi. Hasta se preocupaba de reducir el número de operaciones necesarias en cada cálculo. Por esta razón, aunque no haya sido él el inventor del primer algoritmo, merece que este concepto esté asociado a su nombre.
Aportes
Su obra más importante y por la cual ha sido reconocido en el mundo de las matemáticas es Al-jabar wa´l Muqabala, un tratado sobre como plantear y resolver ecuaciones que involucren problemas de la vida cotidiana.
En la introducción a este texto Abu Abdallah escribe:
Sobre lo que no queda duda es que debemos a su nombre y a su obra maestra términos como álgebra, guarismo y algoritmo.
Un problema de Herón
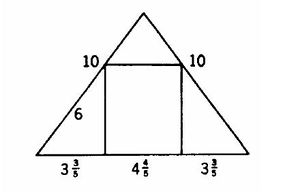
Algunos de los problemas de al-Khwarizmi evidencian con toda claridad, su dependencia de la corriente matemática que proviene de los babilónicos pasando por Herón. Y uno de ellos al menos fue tomado directamente de Herón con gran probabilidad, ya que tanto la figura como las dimensiones son las mismas. Se trata de inscribir un cuadrado en un triángulo isósceles de base 12 unidades y lados iguales de 10 unidades, preguntando el problema la medida del lado de dicho cuadrado. El autor del Algebra calcula en primer lugar, con ayuda del teorema de Pitágoras, la altura del triángulo, 8 unidades así que el área del triángulo es 48.
Llamando al lado del cuadrado "la cosa", se puede ver que se obtendrá el cuadrado de "la cosa" restándole al triángulo grande los tres triángulos pequeños que quedan fuera del cuadrado.
La suma de las áreas de los dos triángulos menores inferiores es evidentemente el producto de "la cosa" por seis menos la mitad de "la cosa" por la mitad de "la cosa"; de todo ello se obtiene facilmente la conclusión de que "la cosa" o lado del cuadrado es 4 4/5 unidades. La diferencia principal entre la forma de este problema en Herón y en Al-Khwarizmi es la de que Herón había expresado la solución en términos de fracciones unitarias como 4 1/2 1/5 1/10. Las analogías son tanto mayores que las diferencias, que podriamos tomar en este caso como una confirmación del principio general de que en la historia de la matemática la continuidad es la regla más que la excepción. Cuando parece presentarse una discontinuidad, lo primero que debemos pensar es que el aparente salto posiblemente se explique por la pérdida de documentos intermedios.
Fuentes
- Varios autores (1974); Grant, E. (ed.): A sourcebook in medieval science. Cambridge (Massachussets): Harvard University Press.
- Al Khwarizmi, 'Abu Ja'far Muhammad ibn Musa (1831). The Algebra of Mohammed ben Musa. traducción, edición y notas de Friedrich Rosen (reimpreso en 1986). Hildesheim: G. Olms Verlag.
- Crossley, John N.; Henry, A. S.. «Thus spake al-Khwarizmi : a translation of the text of Cambridge University Library ms. Ii.vi.5». Historia Math. (1990).
- Gandz, Salomon: The sources of al-Khwarizmi's algebra. Osiris (1936).
- Rashed, Roshdi (1994) (en inglés). The Development of Arabic Mathematics: Between Arithmetic and Algebra. trad. de A. F. W. Armstrong de la edición francesa de 1984. Dordrecht: Kluwer Academic Publishers.
- «Al-Khwarizmi, el álgebra y los algoritmos», artículo publicado en el sitio web Astromia.
- «Al-Khwarizmi», artículo publicado en el sitio web Mimosa.PNTIC.MEC.es.