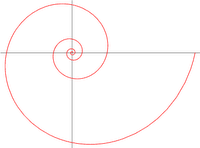
Espiral logarítmica
| ||||||
Espiral logarítmica, es una clase de curva espiral que aparece frecuentemente en la naturaleza. Fue descrita por primera vez por Descartes y posteriormente investigada por Jakob Bernoulli, quien la llamó, "la espiral maravillosa".
Definición
Una espiral logarítmica, espiral equiangular o espiral de crecimiento es la curva definida por un objeto que se mueve con velocidad lineal constante y velocidad angular.
La característica fundamental de esta espiral es que la expansión y la rotación tienen un vínculo geométrico o exponencial. La distancia entre las espiras aumenta mucho más rápidamente que la rotación.
Otros nombres que recibe esta espiral es la de equiangular o geométrica; el primer nombre lo recibe ya que el mismo ángulo de giro, puestos a construirla, crece en progresión aritmética, mientras que el segundo nombre lo recibe por el radio que crece en progresión geométrica.
Este espiral es el que mas podemos observar en la naturaleza, en el reino vegetal, en las formas de las galaxias, en las conchas de algunas especies de moluscos, etc. Es también usado en el arte desde épocas prehistóricas.
Historia
Aparece por primera vez en un escrito de Descartes, en 1638, aunque fue bautizada así por Jakob Bernoulli, en un trabajo suyo donde fascinado por la belleza de esta curva la llama "Spira mirabilis" , tanto le gustó que la hizo grabar en su tumba, pero en vez de poner el dibujo de la espiral logarítmica, pusieron el dibujo de la espiral de Arquímedes .
Jakob Bernoulli escribió que la espiral logarítmica puede ser utilizada como un símbolo, bien de fortaleza y constancia en la adversidad, o bien como símbolo del cuerpo humano, el cual, después de todos los cambios y mutaciones, incluso después de la muerte, será restaurado a su Ser perfecto y exacto
Torricelli estudio sistematicamente las propiedades fundamentales de la espiral logarítmica (llamada por el geométrica), el trazado de cada uno de sus arcos y la cuadratura de la superficie limitada por la curva.
Ecuaciones
- La Ecuación en coordenadas polares (r,θ) es:
r = abθ
o también:
θ=logb(r/a), de aquí el nombre logarítmica.
- La ecuación en forma paramétrica es:
x(θ)=abθcos(θ)
y(θ)=abθsin(θ)
Con números reales positivos a y b. a es un factor de escala que determina el tamaño de la espiral, mientras b controla cuan fuerte y en que dirección está enrollada. Para b >1 la espiral se expande con un incremento θ, y para b <1 se contrae.
Construcción
Para construir una espiral logarítmica se puede proceder de la siguiente forma:
Se construyen sucesivamente rectángulos áureos, es decir trazamos cuadrados dentro de un rectángulo original unas cinco veces obtendremos cinco cuadrados dentro de dicho rectángulo. Si tenemos esto lo que debemos hacer es apoyar un compás en el punto c1, tal cual se muestra en la figura y luego trazar un cuarto de círculo en el cuadrado, de esto forma repetimos este paso en los puntos c2, c3, c4 y c5, obteniendo así la espiral logarítmica.