Óptica Ondulatoria
| ||||||
Óptica Ondulatoria. Principio de Huyghens–Fresnel. Dentro del modelo ondulatorio de la propagación de la luz, el principio de Huyghens – Fresnel es, a su vez, un modelo que permite analizar muchos fenómenos ondulatorios en forma muy sencilla. Durante la propagación de la luz, cada punto de un frente de onda se comporta como un emisor de ondas esféricas secundarias. El nuevo frente de onda creado en un instante Dt posterior pasa por la superficie tangente a las ondas secundarias.
Sumario
- 1 Formación
- 2 Experimento de Young
- 3 Coherencia y Láser
- 4 Interferencia en láminas delgadas
- 5 La Difracción en el Experimento de Young
- 6 Redes de Difracción
- 7 Propiedades de las Redes
- 8 Poder Separador y Dispersión de la Red
- 9 Dispersión
- 10 Absorción de los rayos X
- 11 Polarización de la Luz
- 12 Polarización por Reflexión
- 13 Láminas polaroides
- 14 Birrefringencia
- 15 Prisma de Nicol
- 16 Ley de Malus
- 17 Luz Circularmente Polarizada
- 18 Actividad óptica
- 19 Fuentes
- 20 Enlaces externos
Formación
El nuevo frente de onda se forma a partir de la curva tangente construida a partir de las ondas secundarias, que tienen su centro en un frente de onda determinado. La importancia del principio radica en que, utilizando esta construcción geométrica simple, es posible analizar lo que sucede cuando la luz pasa por un orificio o incide sobre un borde y deja de propagarse en línea recta.
Experimento de Young
Si se iluminan dos rendijas muy unidas y pequeñas con una fuente de luz monocromática, es posible observar en una pantalla, colocada a una distancia adecuada, un conjunto de franjas donde la luz presenta máximos y mínimos alternos de intensidad. Si se hace un gráfico de las intensidades de las franjas en la pantalla .La separación entre franjas está muy exagerada; usualmente el espesor de las franjas no es mayor de una fracción de mm.
El fenómeno mediante el cual aparecen las franjas alternas de luz y sombra se conoce como interferencia de la luz, y puede ser analizado a partir del principio de Huyghens, el concepto de coherencia y el modelo ondulatorio de la luz.
Coherencia y Láser
Un láser (del inglés laser; Light Amplification by Stimulated Emission of Radiation) es un dispositivo luminoso concebido de forma tal que la luz emitida por todos los puntos del foco emisor es coherente. Esta particularidad hace que la luz láser sea extremadamente intensa, muy direccional y con una gran pureza de color (monocromaticidad).
En el láser todos los puntos del foco emiten radiación en fase, lo que no ocurre así en una fuente de luz convencional, donde cada punto radía de forma independiente a los demás.
Existen láseres que trabajan en frecuencias que van desde el infrarrojo hasta los rayos X, y según la sustancia que emplean para generar la luz, los láseres suelen denominarse de estado sólido, de gas, de semiconductores y líquidos. La frecuencia de la radiación emitida depende de la naturaleza de los átomos de la sustancia en cuestión. Los láseres logran emitir luz coherente “estimulando” los átomos de determinadas sustancias. Esos átomos son capaces de "almacenar" la luz proveniente de una fuente externa por un tiempo muy breve y emitirla posteriormente en forma coherente.
Primeramente, los átomos en cuestión son llevados a un estado excitado por la fuente externa; posteriormente esos átomos son estimulados para que emitan la energía almacenada en forma de pulsos de radiación o “fotones”. Los fotones "chocan" a su vez con otros átomos excitados y liberan nuevos fotones. Dos espejos paralelos hacen que los fotones se desplacen continuamente hacia atrás y hacia delante dentro del material desencadenando nuevas emisiones estimuladas y amplificando la luz coherente. Al mismo tiempo, la luz se "filtra" por uno de los espejos, que es sólo parcialmente reflectante, y puede entonces ser utilizada con fines prácticos. El rubí sintético usado en este tipo de láseres se obtiene a altas temperaturas, a partir de una mezcla de óxidos de aluminio y cromo; los iones de Cr3+ son capaces de excitarse con la fuente de xenón y emitir luz roja de gran intensidad. Los posibles usos del láser son casi ilimitados; por ejemplo:
- Industria. En la industria se utilizan como fuente de calor muy localizada. Utilizando lentes es posible enfocar sobre un punto muy pequeño un haz de láser potente, con lo que se logra una enorme densidad de energía. Los haces enfocados pueden calentar, fundir o vaporizar materiales de forma precisa. Por ejemplo, los láseres se usan para taladrar diamantes, modelar máquinas herramientas, recortar componentes microelectrónicas, cortar patrones de modas y sintetizar nuevos materiales.
- Construcciones. También se utilizan láseres para alinear las estructuras en la construcción de carreteras y edificios.
- Geología y Meteorología. Los láseres se emplean para detectar los movimientos de la corteza terrestre y para efectuar medidas geodésicas; también son los detectores más eficaces de ciertos tipos de contaminación atmosférica.
- Astronomía. El láser se ha empleado para determinar con precisión la distancia entre la Tierra y la Luna. La luz de un láser puede viajar largas distancias por el espacio exterior con una pequeña reducción de la intensidad de la señal.
- Comunicaciones. A causa de su alta frecuencia, la luz láser puede transportar, por ejemplo, 1 000 veces más canales de televisión de lo que transportan las microondas, por lo que el láser resulta ideal para las comunicaciones espaciales vía satélite. Se han desarrollado fibras ópticas de baja pérdida que transmiten luz láser para la comunicación terrestre, en sistemas telefónicos y redes de computadoras.
- Medicina. Utilizando haces intensos y estrechos de luz láser es posible cortar y cauterizar ciertos tejidos en una fracción de segundo, sin dañar al tejido sano circundante. El láser se ha empleado para "soldar" la retina, perforar el cráneo, reparar lesiones y cauterizar vasos sanguíneos. También se han desarrollado técnicas láser para realizar pruebas de laboratorio en muestras biológicas pequeñas.
Los láseres han hecho que se pueda determinar la velocidad de la luz con una precisión sin precedentes. También permiten inducir reacciones químicas de forma selectiva y detectar la existencia de trazas muy pequeñas de impurezas en una muestra. El potente y breve pulso producido por un láser también hace posibles fotografías de alta velocidad con un tiempo de exposición de algunas billonésimas de segundo. Finalmente, los sistemas de guiado por láser para misiles, aviones y satélites son muy comunes en la tecnología militar.
Interferencia en láminas delgadas
Es posible ver este tipo de interferencia en el pavimento, cuando después de la lluvia se forma una capa muy fina de grasa o aceite sobre el agua. El fenómeno también se presenta en la membrana de algunas células cuando son observadas al microscopio. Es posible analizar las condiciones en que se presenta el fenómeno,
Condición de mínimo
Supongamos ahora una franja de aceite de espesor variable flotando en el agua. Si la longitud de onda de la radiación incidente es la misma, como el espesor d varía, habrá regiones donde se cumple la condición de máximo y regiones donde se cumple la condición de mínimo. Por tanto, aparecen franjas alternas de luz y sombra. Si en vez de luz monocromática se utiliza luz blanca, diferentes valores de d proporcionarán máximos para las diferentes l presentes, y la superficie se verá coloreada. Esto es justamente lo que sucede en las pompas de jabón, donde el espesor variable de la película jabonosa hace que aparezcan máximos para diferentes l al ser iluminada con la luz natural. El fenómeno se observa bien sólo en láminas muy delgadas, de espesor del orden de 1 mm o menor, equivalente a unas pocas longitudes de onda. Si el espesor de la lámina es grande, la diferencia de recorrido de los rayos varía prácticamente de punto a punto, y lo que ve el observador es un promedio de iluminación de todas las l. Note que la ecuación deducida anteriormente es válida solamente si n2 > n3 y menor que n1. En el caso que n3 fuera mayor que n2 también habría cambio de fase de p en la interfase. La condición de mínimo sería ahora la de máximo, etc.
Difracción
Los patrones de difracción de Fraunhofer se pueden ver directamente, pues el cristalino del ojo funciona como lente convergente y el cristalino como pantalla.
Las lentes no añaden diferencias de fase adicional a las ondas que las atraviesan por diferentes puntos. Es cierto que, en una lente convergente, el rayo de luz que pasa por el centro recorre una distancia mayor que el que pasa por el borde de la lente, pero lo hace con velocidad v = c/n < c. Así, el rayo que pasa por el centro recorre una distancia mayor, pero a menor velocidad, mientras que el que pasa por el borde recorre sólo una distancia pequeña a menor velocidad, y el resto a mayor velocidad. El resultado neto es que ambos efectos se compensan y no se introduce diferencia adicional.
La Difracción en el Experimento de Young
En la parte superior, el patrón de difracción de una de las rendijas en un experimento de Young. En la parte inferior aparece el patrón de interferencia producido por las dos rendijas. Las franjas de interferencia no pueden aparecer en las regiones donde la difracción no permite la llegada de la luz. Se dice entonces que el patrón de interferencia está modulado por el patrón de difracción.
Redes de Difracción
Una red de difracción es un sistema óptico similar al del experimento de Young, pero con miles de rendijas por cm.
Las redes se construyen de diferentes formas (por ej., rayando vidrio con máquinas muy precisas o por métodos fotográficos de reducción de una imagen a rayas). Si l es la longitud de la red y N el número de ranuras, la distancia entre ranura vendrá dada por El inverso de esta distancia (1/d) es la constante de la red (número de ranuras por cm). Cuando se hace incidir luz monocromática sobre una red de difracción, se obtiene un patrón de interferencia similar al del experimento de Young, pero mucho más intenso. La condición de máximo de interferencia es la misma que en el experimento de Young: dsenq = ml
En realidad, esta es la expresión de los máximos principales porque también aparecen pequeños máximos secundarios de muy poca intensidad, y que no serán tomados en cuenta en el análisis posterior.
Propiedades de las Redes
Los máximos principales cumplen la condición dsenq = ml, donde d es la distancia entre ranuras. La distancia entre máximos también es similar a la del experimento de Young; Dx = lL/d.
Mientras mayor sea el número N de franjas iluminadas, más intensos y estrechos serán los máximos sin que su posición angular varíe.
Cuando N es del orden de miles de rendijas por cm, se obtienen líneas muy estrechas, con un ensanchamiento mínimo.
Junto a los prismas, las redes de difracción son muy utilizadas en los espectrógrafos para obtener los espectros de fuentes luminosas. Usualmente tienen un poder de dispersión mayor que los prismas y permiten analizar un intervalo mayor de longitudes de onda.
Poder Separador y Dispersión de la Red
Poder Separador
En el espectro de 1er orden de la sección 7.8, considere los máximos correspondientes a dos longitudes de onda muy cercanas, l1 y l2. Si los dos máximos se encuentran muy unidos, no es posible distinguir o “separar” una longitud de onda de la otra. Se acostumbra considerar que las líneas están separadas cuando cumplen el criterio de Rayleigh.
El criterio de Rayleigh establece que las líneas correspondientes a dos diferentes l pueden considerarse resueltas o separadas a partir de que el máximo de una de ellas coincida con el 1er mínimo de difracción de la otra. El poder separador de la red se define por la expresión R =
Donde l = ½ (l1+l2). Es posible demostrar que, para ángulos pequeños, el poder separador de la red depende del número de rendijas iluminadas por la expresión R = Nm ,donde m es el orden del espectro.
Dispersión
Otro parámetro característico de la red es su dispersión, definida como D = dq/dl. Se deja al lector la tarea de demostrar, derivando en la condición de máximo, que la dispersión de la red resulta ser igual a Esta expresión indica que las líneas estarán más separadas mientras menor sea la separación d entre rendijas y también mientras mayor sea el ángulo de dispersión q.
Difracción de Rayos X En 1912 el alemán Max Von Laue encontró que al hacer incidir una haz de radiación de rayos X no monocromático sobre un cristal de sal común (NaCl) aparecía un patrón de difracción característico, que podía ser recogido en una placa fotográfica. Este experimento permitió verificar dos cosas muy importantes, desconocidas hasta el momento:
La naturaleza ondulatoria de los rayos X, que habían sido descubiertos por Röentgen en 1895 sin que se lograra determinar de qué estaban compuestos. La estructura periódica de los cristales, lo que hoy día se conoce como estructura cristalina de las sustancias sólidas.
Un cristal es un arreglo ordenado de átomos o moléculas, que se repite periódicamente en el espacio. La celda elemental del cristal es la mínima unidad mediante la cual el cristal se pude construir por repetición tridimensional. En el NaCl la celda elemental es cúbica, de longitud a = 5.62 Å , y contiene iones alternos de Cl- y Na+ (cristal iónico).
La unión de los átomos que se encuentran en un mismo plano forma los llamados planos cristalinos. Cada cristal posee múltiples familias de planos cristalinos, con diferentes distancias interplanares. La difracción de la radiación en los cristales sólo tiene lugar cuando el tamaño de longitud de onda es del orden de las distancias interplanares del cristal (l ~ a). Esta longitud de onda, del orden de unos pocos ángstrom, corresponde a la región de los rayos X. Es posible encontrar las direcciones de los rayos difractados en el experimento de Laue de una forma muy sencilla; considerando que cada familia de planos se comporta como un conjunto de espejos semiplateados. En la realidad, cada átomo se comporta como un emisor de ondas secundarias, a causa de la oscilación de los electrones excitados por la radiación incidente. Las ondas secundarias interferirán, dando máximos de difracción en determinadas direcciones.
La condición de máximo, que presentamos sin demostración, es 2dsenq = ml donde d es la correspondiente distancia interplanar y q el ángulo formado por el plano y la radiación incidente.
Esta expresión se conoce como Ley de Bragg. En el experimento de Laue, realizado con radiación no monocromática, se observa un haz difractado siempre que l, q y d sean tales que se cumpla la ley de Bragg
Absorción de los rayos X
Los rayos X de longitud de onda larga, mucho mayor que las distancias interplanares, no se difractan al incidir sobre la sustancia, pero tienen la propiedad de atravesar en mayor o menor grado los cuerpos opacos a la luz visible.
De aquí que el uso más extendido de los rayos X haya sido como herramienta de diagnóstico médico. La absorción de los rayos X será mayor allí donde la sustancia sea más densa (huesos) mientras que la radiación que incide sobre los tejidos blandos pasa con mucha mayor facilidad. Utilizando una placa fotográfica es posible obtener fotografías (radiografías) donde se observa perfectamente el contraste entre los huesos sombreados y los tejidos blandos. Como en el negativo fotográfico se invierte la coloración, los huesos se ven blancos y los tejidos blandos más oscuros.
Para obtener rayos X se utilizan tubos al vacío donde los electrones emitidos por un cátodo son frenados bruscamente en un ánodo. El frenaje brusco de los electrones produce la emisión de rayos X y calor. Regulando la velocidad de los electrones, la naturaleza del cátodo y utilizando filtros es posible obtener radiaciones de diferentes longitudes de onda. En noviembre de 1895, Wilhelm Conrad Roentgen (1845 - 1923) trabajaba en su laboratorio de la universidad de Würzburg, en Alemania, estudiando los efectos de pasar una corriente eléctrica a través de un gas a presiones muy bajas. Al llevar a cabo sus observaciones, notó que su dispositivo ocasionaba la fluorescencia de sales de platino cianuro de bario que se encontraban sobre su mesa de trabajo. Después de realizar una serie de experimentos cuidadosos, llegó a la conclusión de que había descubierto un nuevo tipo de radiación, a la que llamó “rayos X”. Al investigar la capacidad de penetración de estos nuevos rayos, Roentgen puso una placa fotográfica debajo de la mano de su mujer y registró así la primera “placa” de rayos X de la historia.
Polarización de la Luz
La luz ordinaria es no polarizada, tanto si es natural como artificial. Significa esto que si, colocados de frente a la fuente de luz, fuéramos capaces de medir el vector intensidad de campo eléctrico a lo largo de una dirección determinada, obtendríamos algo similar a lo representado en la figura: cualquiera que sea la dirección del espacio que se escoja para medir , se obtendría el mismo valor.
Dicho de otra forma, la componente del vector intensidad de campo tiene el mismo valor en todas las direcciones.
Por el contrario, si se logra obtener luz donde el vector intensidad de campo vibre siempre en una sola dirección, decimos que la luz está polarizada en un plano. También es posible la existencia de la luz parcialmente polarizada, en la que el vector intensidad de campo tiene un valor mayor en determinada dirección, pero no se anula totalmente en la dirección perpendicular.
Existen diferentes formas de obtener luz polarizada. A continuación se describen algunas de ellas.
Polarización por Reflexión
Cuando la luz se refleja o se refracta en cualquier superficie, se polariza en mayor o menor grado. El grado de polarización depende del ángulo de incidencia. Se ha encontrado que existe un cierto ángulo de incidencia qB donde tanto la luz reflejada como la refractada salen totalmente polarizadas. Ese ángulo se denomina ángulo de Breaster. Es posible demostrar que en ángulo de Brewster viene dado por la expresióntan qB = donde n1 es el índice de refracción del medio de donde proviene la luz. También se demuestra que cuando el ángulo de incidencia es igual al ángulo de Brewster, para el rayo refractado se cumple que qB + q2 = 90o.
Láminas polaroides
Los cristales de sulfato de iodo-quinina poseen anisotropía cristalina. Significa que sus propiedades ópticas son diferentes en dependencia de la dirección de propagación relativa a sus ejes cristalográficos. Estos cristales absorben la luz selectivamente, en dependencia de la dirección del vector intensidad de campo E respecto a esos ejes. El fenómeno se conoce como dicroísmo.
Las láminas polaroides se construyen de algún tipo de plástico transparente, con la adición de microcristales de sulfato de iodo-quinina. Los cristales se someten a un proceso de orientación por estiramiento, de manera tal que todos quedan orientados en la misma dirección. Así, al atravesar una lámina polaroide, la luz es absorbida con mayor intensidad a lo largo de determinadas direcciones, y la fracción que logra atravesar la lámina queda polarizada en un plano.
La dirección de la lámina a la cual el vector E sale paralelo se denomina eje óptico de la lámina.
Birrefringencia
Muchos sólidos cristalinos poseen diferentes propiedades físicas a lo largo de diferentes direcciones. En el esquema de un sólido cristalino representado en la figura, no es lo mismo “moverse” a lo largo de la dirección (1) que a lo largo de (2). Las distancias entre planos atómicos y átomos iguales no son las mismas, ni tampoco lo es la interacción de los átomos vecinos.
Esta anisotropía da lugar a que, en algunos cristales y en determinadas condiciones, un solo rayo incidente de lugar a dos rayos refractados. El fenómeno se conoce como doble refracción ó birrefringencia. Cuando hay birrefringencia, a partir de un rayo incidente ri aparecen dos rayos refractados: el rayo ordinario y el rayo extraordinario El rayo ordinario (ro) cumple la ley de Snell. El rayo extraordinario (re) no cumple la ley de Snell (ni siquiera está en el mismo plano que los otros dos). Ambos rayos están polarizados en direcciones perpendiculares y tienen diferente velocidad de propagación. Significa que no ¹ ne. En general, el índice de refracción extraordinario ne depende de la dirección. El valor de ne que difiere más de no es el índice principal de refracción del rayo extraordinario. Algunos cristales necesitan de tres índices de refracción para describir su comportamiento.
Prisma de Nicol
El prisma de Nicol es un dispositivo que se utiliza para obtener luz polarizada, basado en el fenómeno de la birrefringencia. Se construye pegando dos prismas de calcita transparente monocristalina con resina del abeto balsámico del Cánada (bálsamo del Canadá) que posee un alto índice de refracción (n = 1.55). El eje óptico del cristal es aquel que, cuando la luz viaja en esa dirección, no se polariza.
Ley de Malus
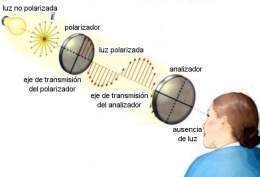
Considere un dispositivo polarizador, construido con dos nicoles o con láminas polaroides.
Interesa calcular la relación entre las intensidades antes y después de pasar el analizador. Para ello se considera que la lámina polaroide sólo deja pasar la componente de Eo que se encuentra a lo largo del eje óptico. Los sistemas polarizadores – analizadores se utilizan en instrumentos tales como polarímetros y sacarímetros, analizados en las secciones siguientes.
Luz Circularmente Polarizada
En determinadas condiciones es posible obtener un rayo de luz donde el vectordescriba una circunferencia al transcurrir el tiempo. Esto se logra haciendo pasar luz polarizada por un cristal birrefringente, con el eje óptico orientado adecuadamente y de un espesor tal que el rayo ordinario y el extraordinario, que tienen diferentes velocidades de propagación, salgan perpendiculares entre sí y con una diferencia de fase de p/2.
Para demostrar que la composición de estos dos rayos proporciona un vector que describe una circunferencia, analicemos cuáles son las componentes de un vector que rota con velocidad angular constante w alrededor de un eje fijo, como se muestra en la figura. Se considera que f = (kr - wt), donde r es la distancia a lo largo de la dirección de propagación, constante en un punto determinado.
A dos ondas polarizadas en un plano que se propagan en dirección perpendicular al plano del papel, con igual amplitud, perpendiculares entre sí, y con diferencia de fase de p/2, como se había señalado anteriormente. Es posible considerar la luz polarizada en un plano como formado por la superposición de dos ondas circularmente polarizadas que giran en sentido contrario, con la misma velocidad angular e igual amplitud. Esta representación es útil para explicar determinados fenómenos, como se verá a continuación.
Actividad óptica
Existen sustancias que tienen la propiedad de hacer rotar el plano de polarización cuando la luz las atraviesa. Se denominan sustancias ópticamente activas, y pueden ser tanto líquidas como sólidas. En el caso de los sólidos se destaca el cuarzo, mientras que en los líquidos pueden mencionarse el alcohol amílico, las disoluciones de ácido tartárico, de glucosa, sacarosa y levulosa. Las sustancias ópticamente activas también pueden ser dextrógiras o levógiras, en dependencia de si el plano de polarización rota a la derecha o a la izquierda cuando el observador se encuentra de frente a la fuente de luz.
El coeficiente a se denomina rotación específica de la sustancia en cuestión y depende, en general, de la longitud de onda y de la temperatura. Por esta razón, los valores que aparecen tabulados en los manuales usualmente vienen reportados para la luz de sodio de 589 nm, una lámpara de uso muy extendido en el trabajo de laboratorio.
El instrumento que se utiliza para medir el ángulo rotado en disoluciones es el polarímetro, cuyo esquema se muestra a continuación. El instrumento posee escalas en el ocular que permiten determinar el angulo rotado. Se opera haciendo girar el analizador hasta la posición de máxima penumbra antes y después de colocar el vaso polarimétrico con la disolución a analizar. Un sacarímetro es un tipo especial de polarímetro diseñado especialmente para determinar concentraciones de sacarosa.
El instrumento que se utiliza para medir el ángulo rotado en disoluciones es el polarímetro, cuyo esquema se muestra a continuación. El instrumento posee escalas en el ocular que permiten determinar el angulo rotado. Se opera haciendo girar el analizador hasta la posición de máxima penumbra antes y después de colocar el vaso polarimétrico con la disolución a analizar. Un sacarímetro es un tipo especial de polarímetro diseñado especialmente para determinar concentraciones de sacarosa.
La actividad óptica en las disoluciones depende del arreglo espacial de los átomos en las moléculas de la sustancia disuelta. Estas moléculas, que no tienen centros o planos de simetría, poseen una simetría particular que hace que la luz circularmente polarizada con diferentes sentidos de rotación atraviese la sustancia con diferente velocidad (moléculas enantiomorfas). El considerar la luz polarizada en un plano como formada por dos haces de luz circularmente polarizada, rotando en sentidos contrarios, permite dar una explicación simple a la rotación del plano de polarización.
La actividad óptica en las disoluciones depende del arreglo espacial de los átomos en las moléculas de la sustancia disuelta. Estas moléculas, que no tienen centros o planos de simetría, poseen una simetría particular que hace que la luz circularmente polarizada con diferentes sentidos de rotación atraviese la sustancia con diferente velocidad (moléculas enantiomorfas). El considerar la luz polarizada en un plano como formada por dos haces de luz circularmente polarizada, rotando en sentidos contrarios, permite dar una explicación simple a la rotación del plano de polarización.