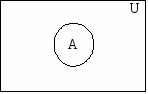
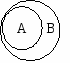
Diagrama de Venn
| ||||||
Diagrama de Venn. En Matemáticas y Teoría de conjuntos dícese de la representación gráfica que a base normalmente de círculos y rectángulos, superpuestos o no, ilustra las relaciones y operaciones entre los conjuntos.
Los mismos fueron ideados por el matemático y filósofo inglés John Venn hacia julio de 1880 con la publicación de su trabajo titulado "De la representación mecánica y diagramática de proposiciones y razonamientos" en el Philosophical Magazine and Journal of Science, lo cual provocó gran revuelo en el mundo de la lógica formal.
Definición
Estas son las representaciones según los diagramas de Venn de los distintos componentes de la teoría de conjuntos y sus operaciones:
Historia
Los diagramas de Venn se deben a John Venn, matemático y filósofo inglés, quien hacia julio de 1880 publicó en el Philosophical Magazine and Journal of Science el trabajo titulado "De la representación mecánica y diagramática de proposiciones y razonamientos" , provocando un gran revuelo en el mundo de la lógica formal.
Pese a que Leibniz, Boole y Augustus de Morgan habían desarrollado formas previas de representación geométrica de silogismos lógicos, Venn superaba en claridad y sencillez los sistemas de representación de aquellos, consiguiendo convertirse a la larga en el nuevo estándar, pues entre otras particularidades. Venn fue el primero en formalizar su uso, ofreciendo un mecanismo de generalización de los mismos.
Su libro Lógica simbólica, de 1881 aunque no tuvo demasiado éxito en su empeño de interpretar y corregir los trabajos de Boole en la lógica formal; se convirtió en una excelente plataforma de ejemplo para el nuevo sistema de representación. Tras su siguiente libro "Los principios de la lógica empírica", de 1889, los diagramas de Venn fueron cada vez más empleados como representación de relaciones lógicas.
Los diagramas de tres conjuntos fueron los más corrientes elaborados por Venn en su presentación inicial y aunque estaba apuntado en sus trabajos la representación gráfica del conjunto universo la idea actual del mismo se atribuye a Lewis Carroll, matemático y escritor de Alicia en el país de las maravillas.
Ejemplos
| Álgebra conjuntual | Diagrama de Venn |
|---|---|
| A'=U-A | 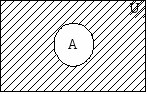
|
| ( |
|
| Archivo:Complemento A unido B.gif | 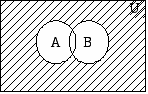
|
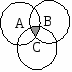
|
Consecuencias
Los diagramas de Venn aportan mayor legibilidad y comprensión a la teoría de conjuntos y al álgebra de los mismos. Contribuye de forma bien ilustrativa a representar relaciones que de otra manera resultan más abstractos y de esa forma pueden mostrarse a estudiantes de grados inferiores en la enseñanza general. También resultaron como la extensión de trabajos previos en el mismo terreno o similares de la lógica formal que al final trascendió por su simplicidad y valor práctico.
No obstante, aparecen deficiencias a la hora de tratar con relaciones algebracias de más de tres conjuntos para los cuales se ha propuesto soluciones como las extensiones de Edwards.
Véase también
Fuentes
- Significado del Diagrama de Venn
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir. Moscú, 1988.
- Diagramas de Venn en Wikipedia. Consultado el 1 de diciembre de 2013.