Sir Willian Rowan Hamilton
| ||||||||||||||||||||
Sir William Rowan Hamilton. Fue un matemático, físico y astrónomo irlandés, que hizo importantes contribuciones al desarrollo de la óptica, la dinámica, y el Álgebra.
Sumario
Síntesis biográfica
Nació el 4 de agosto de 1805 y falleció el 2 de septiembrede 1865, conocido sobre todo por sus trabajos en análisis de vectores y en óptica. Nació en Dublín y estudió en el Trinity College. En 1827, sin haber obtenido su título, fue nombrado profesor de astronomía, y al año siguiente astrónomo real para Irlanda. Hamilton pasó el resto de su vida trabajando en el Trinity College y en el observatorio de Dunsink, cerca de Dublín. En el campo de la dinámica, introdujo las funciones de Hamilton, que expresan la suma de las energías cinética y potencial de un sistema dinámico; son muy importantes en el desarrollo de la dinámica moderna y para el estudio de la teoría cuántica. Describió una forma matemática de manejar pares de números reales.
Esas reglas se usan en la actualidad para operar con números complejos. Más adelante descubrió la clave para operar con ternas o n-uplas de números, en el caso de n2, que consistiía en descartar la propiedad conmutativa de la multiplicación usual. A los nuevos objetos que creó les llamó cuaterniones, precursores de lo que ahora son los vectores. Su monumental obra acerca de este tema, Treatise on Quaternions, fue publicada en 1853.
Obra matemática
El matemático más eminente de los pueblos de habla inglesa, después de Isaac Newton, es William Rowan Hamilton, que nació en 1805 y murió en 1865. Su fama ha sufrido vicisitudes curiosas. Durante su vida fue aclamado, pero no entendido. Después de su muerte su reputación empezó a declinar y se llegó a ser tenido como figura de segunda categoría. En el siglo XX ha tenido lugar una revitalización extraordinaria del interés y la estima por él.
Acerca de sus antepasados no hay mucho que decir. Su padre era un abogado de Dublín, que defendió al patriota irlandés Archibald Hamilton Rowan y obtuvo una revocación de su sentencia. De Rowan que actuó como padrino en el bautismo de William, el niño recibió su segundo nombre. No fue educado por sus propios padres. Cuando tenía alrededor de un año decidieron confiar su educación al hermano James del Señor Hamilton, un clérigo establecido en Trim, una pequeña ciudad treinta millas al norte de Dublín. El joven William vivió en Trim, con visitas ocasionales a Dublín, hasta que tubo la edad de ingresar en la Universidad.
Debido a los métodos educativos de su tío o a sus propios dones naturales, lo cierto es que se cuenta que a la edad de tres años William podía leer ya inglés fácilmente. A los cinco era capaz de traducir latín, griego y hebreo. A los ocho había añadido el italiano y el francés a su lista. Antes de tener diez años estaba ya estudiando árabe y sánscrito. A la edad de catorce escribió una carta en persa al embajador persa, entonces de visita en Dublín.
Al niño le gustaba los clásicos y los poetas; pero a la edad de quince años sus intereses y el curso de su vida fueron transformados cuando se encontró con un tal Zerah Colburn, un joven americano que presentó en Dublín una exhibición de su potencia como calculador rápido. Durante largo tiempo después, escribió Hamilton más tarde: "Me aficioné a realizar largas operaciones aritméticas mentalmente. Extraía raíces cuadradas y cubicas y meditaba todo lo relacionado con las propiedades de los números." William se decidió a dedicar su vida a las matemáticas. "Nada", afirmó más tarde, "ensalza la mente de igual manera o eleva al hombre de sus iguales como las investigaciones de la ciencia. ¿Quién es el que no preferiría tener la fama de Arquímedes que la de su conquistador Marcelo?... Espíritus poderosos de todas las edades han colaborado para construir este templo amplio y bello de la ciencia y han escrito sus nombres sobre con caracteres indelebles. Pero el edificio no está aún completo. Aún no es demasiado tarde para añadir otro adorno. Yo todavía apenas he llegado a su base, pero puedo aspirar un día a alcanzar su ápice.
En su diario aparecen continuamente tales anotaciones, como "leí la Vida de Newton" y "comencé los Principios de Newton". A los dieciséis años se familiarizó con la Mecánica Celeste de Laplace (una nota en su diario alrededor de esta época dice así: "Nos hemos estado levantando antes de las cinco varia de estas mañanas mi tío y yo. El tira de un cordel que va a través de la pared y está atado a mi camisa de noche"). En 1823, precedido por los rumores de su potencia intelectual, "Hamilton el prodigio" ingresó en el Trinity College de Dublín. Allí su progreso fue brillante no solamente en los exámenes, sino también en investigación original. Cuando tenía tan solo veintiún años presentó un artículo al Academia Real Irlandesa titulado: "Una teoría de sistemas de rayos", que, en efecto, convirtió la óptica matemática en una nueva ciencia.
Si bien todo el mundo reconocía la grandeza del honor sin precedentes del nombramiento de Hamilton a dicha cátedra, la opinión estaba fuertemente dividida con respecto a su prudencia en aceptarla. Tras un año o dos hubiera sido elegido, sin duda, profesor (fellow) de Trinity College, con mejores perspectivas económicas y generales. Lo que determinó su elección fue la consideración de que el puesto de Astrónomo Real era prácticamente un nombramiento de investigación, que implicaba muy poco con respecto a tareas fijas, mientras que un fellow en el Trinity College debía convertirse en clérigo y se hubiera pronto transformado en tutor y lector, con deberes fijos que ocuparían la mayor parte de su tiempo. Era cierto que el equipo de nvestigación del observatorio astronómico era enormemente pobre; pero lo que realmente estaba en la mente de Hamilton, así como en la de los electores, no era la astronomía, sino un arreglo por el que Hamilton pudiera continuar las investigaciones teóricas de las que el artículo sobre los Sistemas de Rayos había sido un glorioso comienzo.
Hamilton tubo en realidad el deber de dar un curso de lecciones sobre astronomía. En éstas, su costumbre era discutir las relaciones de la astronomía con la ciencia física en general, con la metafísica y con todos los campos relacionados del saber. Sus lecciones eran tan poéticas y tan cultas que pronto trajeron audiencias enormes de profesores y visitantes, así como también sus lecciones a subgraduados. Cuando en 1.831 se empezó a hablar de su traslado a la cátedra de matemáticas, el Consejo insistió en que permaneciera donde estaba. Como incentivo, el Consejo subió su pensión a 580 libras al año y le dio permiso para dedicar su investigación principalmente a las matemáticas.
En 1832, Hamilton anunció a la Academia Real de Irlanda un descubrimiento en óptica notable, que prosiguió su teoría de los sistemas de rayos. Se sabía desde hacía algún tiempo que ciertos cristales biaxiales, tales como el topacio y la aragonita, daban lugar a dos rayos refractados, produciendo una doble imagen. Agustín Fresnel había elaborado las leyes de la refracción doble. Ahora Hamilton, investigando por su método general la ley de Fresnel, llegó a concluir que en ciertos casos, un único rayo de luz incidente sobre un cristal biaxial puede dar lugar no solamente a dos, sino a un número infinito de rayos refractados, formando un cono, y que en otros ciertos casos un único rayo dentro de tal cristal emergería de él como un cono diferente. Propuso, por consiguiente, partiendo de consideraciones teoréticas, dos nuevas leyes de la luz, que él llamó de refracción cónica interna y externa. Pronto fueron verificadas experimentalmente por su amigo Humphrey Lloyd, un físico de Dublín.
En 1834, Hamilton, que entonces tenía veintinueve años, escribió a su tío: "Es mi propósito y mi esperanza remodelar todo el conjunto de la dinámica, en el sentido más extenso de la palabra, por medio de la idea de mi función característica". Procedió entonces a aplicar este principio al movimiento de sistemas de cuerpos, y al año siguiente expresó las ecuaciones del movimiento en una forma que demostraba la dualidad entre las componentes del momento de un sistema dinámico y las coordenadas de su posición. Fue un siglo más tarde cuando el desarrollo de la teoría cuántica permitió a físicos y matemáticos darse perfecta cuenta de la importancia de esta dualidad. En 1835, Hamilton recibió el honor de ser nombrado caballero, y dos años más tarde fue elegido presidente de la Academia Real Irlandesa. Pero su vida privada fue menos feliz.
Después de haberse convertido en profesor había establecido su casa con tres de sus hermanas en el observatorio de Dunsink, sobre una colina a cinco millas de Dublín. A la edad de veintiséis años se enamoró de Helen María Bayly, la hija de un antiguo rector en el condado de Tipperay. Al principio ella rehusó aceptar a su proposición de matrimonio, pero, finalmente, la aceptó y la boda tuvo lugar el nueve de Abril de 1833. Escribiendo acerca de ella en una carta a un amigo, Hamilton hacía notar su "extraordinaria timidez y delicadeza". Estas características llegaron a agudizarse más plenamente después del matrimonio. Lady Hamilton dio a luz a dos hijos y una hija en seis años, pero no se encontró preparada para el trabajo de la administración doméstica, y dejó Dunsink durante dos años para vivir con una hermana casada en Inglaterra. Volvió en 1842, pero las cosas no mejoraron. Desde entonces, Hamilton no tenía tiempos establecidos para sus comidas y pronto empezó a utilizar estimulantes alcohólicos en un grado peligroso.
Cuando yo ocupé la cátedra de Hamilton, para la cual tuve el honor de ser nombrado en 1906, muchos años después de su muerte, encontré a mucha gente que le había conocido. El país estaba lleno de historias acerca de él. Una de ellas se refiere a la administración de los diecisiete acres de granja alrededor del observatorio de Dunsink, sobre los cuales el Astrónomo Real tenía control. Hamilton, que había sido educado en la ciudad, no sabía nada de granjas; pero a fin de proporcionar leche para su casa compró una vaca. Tras algún tiempo, como era natural que aconteciese, la producción de leche comenzó a decaer. Hamilton fue a consultar a un granjero vecino. El granjero, sabiendo con quién se las veía, le dijo que la vaca, como único ocupante de diecisiete acres, sufría de soledad. Hamilton entonces le preguntó si sería posible proveerla de compañeros, y el granjero se puso de acuerdo con satisfacción, a cambio de un pago conveniente por Hamilton, en permitir a su ganado pastar en los abundantes pastos de Dunsink.
A pesar de las condiciones desfavorables de su vida, el trabajo científico de Hamilton continuó. En 1843 hizo un gran descubrimiento, el cálculo de cuaternios.
Fue llevado a este descubrimiento trabajando prolongadamente sobre el problema de buscar una regla general para calcular la cuarta proporcional, dados tres segmentos rectilíneos, cuando las direcciones de estos segmentos han de ser tenidos en cuenta. Un segmento rectilíneo con una dirección fijada se llama vector. Era ya conocido que un vector en un plano podía ser representado por un número complejo, esto es, un número formado por números a la vez reales e imaginarios de la forma x + y · . Si representamos los números reales como distancias sobre el eje x de una gráfica, entonces la multiplicación de un número cualquiera por -1 , transformándolo en un número negativo si es positivo, puede considerarse como una rotación del segmento rectilíneo de 180 grados; mientras que la multiplicación por i , puede ser considerada como una rotación de 90 grados.
Los números complejos
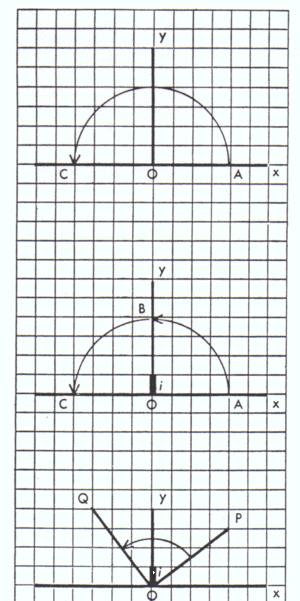
EL NÚMERO COMPLEJO, compuesto de un número real y otro imaginario, la raíz cuadrada de -1, se usa para describir la longitud y dirección de un segmento rectilíneo. El proceso de adición, sustracción o multiplicación de números complejos es equivalente a una operación geométrica, por ejemplo, rotación. En el diagrama de la parte superior el segmento OA, representa el número +4, se multiplica por -1, lo cual lo transforma en el segmento OC, es decir, -4. Así la multiplicación por -1 es equivalente a una rotación de 180 grados. En el diagrama de en medio la multiplicación por -1 se lleva a cabo en dos etapas, multiplicamos primero por i (i es la raíz cuadrada de -1) y luego otra vez por i. Por consiguiente, la multiplicación por i se puede considerar como una rotación de 90 grados. Esto conduce a la idea de medir distancias imaginarias sobre el eje y, como se indica, tomando "i" como vector unitario sobre dicho eje. El diagrama de la parte inferior muestra que la multiplicación por i tiene el efecto de una rotación de 90 grados, aunque el punto de partida no esté sobre el eje x. El segmento que va de O(x=0,y=0) al punto P(x=4,y=3) se representa en notación compleja como 4+3i. Al multiplicar este número por i resulta 4i+3i2, es decir, 3-4i. Este número representa el segmento OQ(x=-3,y=4), es decir, la rotación de 90 grados del segmento OP.
De esta forma, los números imaginarios son representados sobre el eje y , e i puede ser considerado como una unidad sobre este eje o un "vector unitario". Todo vector sobre un plano puede entonces ser determinado por un número complejo, dando sus componentes x e y. Un par de números de esta forma obedece las misma leyes algebraicas que un único número. Pares así pueden ser sumados, restados, multiplicados y divididos según las leyes usuales. Así es posible calcular la cuarta proporcional a tres vectores en un plano común: V1 : V2 = V3 : x
Llegó a conjeturar que en el espacio de tres dimensiones un vector podría ser representado por un conjunto de tres números, de la misma forma que un vector en un plano es expresado en un par. Trató de encontrar la cuarta proporcional multiplicando ternas, conjuntos de tres números, pero encontró dificultades. Los miembros más jóvenes de la casa de Dunsink participaban con afecto en las esperanzas y desengaños de su ilustre padre, a medida que las investigaciones tenían lugar. William Edwin, de nueve años y Archibald Henry, de ocho solían preguntar en el desayuno: "¿Qué, papá, puedes multiplicar ya ternas?" A lo cual se veía obligado a contestar, sacudiendo tristemente su cabeza: "No, sólo los puedo sumar y restar". Un día, paseando de Dunsink a Dublín, Hamilton se dio cuenta repetidamente de la respuesta. Las operaciones geométricas de los espacios de tres dimensiones requerían para su descripción no conjunto de tres, sino de cuatro números. A fin de especificar la operación necesaria para convertir un vector en otro en el espacio, era necesario conocer cuatro números: (1) la relación entre la longitud de un vector y la del otro, (2) el ángulo entre ellos, (3) el nodo y (4) la inclinación del plano en el que estos vectores se encuentran.
Denominó el conjunto de cuatro números un cuaternio y encontró que podía multiplicar cuaternios como si fuesen números. Pero descubrió que el álgebra de los cuaternios era diferente del álgebra ordinaria en un aspecto crucial. Era no conmutativa. Esta denominación requiere alguna explicación. Cuando multiplicamos 2 por 3 obtenemos el mismo producto que si multiplicamos 3 por 2. Esta ley conmutativa de multiplicación, como se llama, viene simbolizada en la fórmula algebraica ab = ba . Se aplica a números imaginarios tanto como a los reales. Sin embargo, no vale para el cálculo de los cuaternios, porque este último describe operaciones geométricas, tales como rotaciones
El Álgebra No Conmutativa
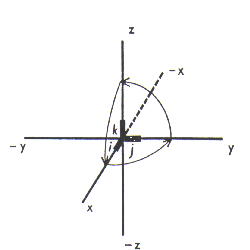
EL ÁLGEBRA NO CONMUTATIVA, se utiliza para representar operaciones geométricas en tres dimensiones. Un vector tridimensional se representa en un sistema de coordenadas con tres ejes mutuamente perpendiculares (x se dirige hacia el lector, y y z están en el plano de la página) en función de los vectores unitarios i, j, k. La multiplicación por i se define convencionalmente como una rotación de 90 grados en el plano perpendicular al vector i, es decir, en el plano de y y z. La multiplicación por j y por k se define de modo análogo, como se indica por las flechas. Entonces se puede observar que al aplicar i a j, es decir al formar i x j resulta que se gira j para obtener k. Por otra parte, al aplicar j a i, es decir al formar el producto j x i , resulta que se gira i para obtener -k. Así tenemos i x j = k, y j x i = -k. Es decir, que la multiplicación no es conmutativa. El producto i x j no es igual al producto j x i.
Representan tres ejes mutuamente ortogonales, pudiéndose uno imaginar que los ejes y y z están en el plano del papel y que el eje x se dirige hacia el lector. Los símbolos i , j y k , representan vectores unitarios a lo largo de los ejes x , y y z , respectivamente. La multiplicación por i se define como una rotación en sentido contrario a las agujas del reloj de noventa grados, en el plano del papel. La multiplicación de j y por k son rotaciones en planos perpendiculares a aquel plano. Ahora bien la multiplicación de j por i hace girar j para llevarlo a k , es decir, i·j=k . Pero la multiplicación de i por j hace girar i para llevarlo a -j , es decir j·i=-k . Así i·j no es igual a j·i.
El abandono de la ley conmutativa fue una tremenda ruptura con la tradición. Señaló el comienzo de una nueva era. Las noticias del descubrimiento se extendieron rápidamente y produjeron en todo caso en Dublín una ola de interés entre la gente de alcurnia y elegancia, semejante a la otra más reciente acerca de la relatividad general en Londres, cuando Lord Haldane invitó a Einstein a tomar el lunch con el arzobispo de Canterbury. Hamilton se encontró abordado en la calle por miembros de la aristocracia angloirlandesa, con la pregunta: "¿Qué diablos son los cuaternios?" Para satisfacerlos publicó la deliciosa Carta a una señora en la cuál explicaba que el término "aparece", por ejemplo, "en nuestra versión de la Biblia, donde el apóstol Pedro se dice haber sido entregado por Herodes a la custodia de cuatro cuaternios de soldados...", y para presentar una comparación más moderna y menos solemne, aparecida en las páginas de Guy Mannering, Scott representa a Robert Hazelwood of Hazelwood como recargando sus largas frases con "tríadas y cuaternios".
Desde este tiempo hasta su muerte, veintidós años más tarde, el principal interés de Hamilton fue desarrollar el nuevo cálculo. Fueron años preponderantemente tristes y solitarios, debidos a enfermedades frecuentes y a las ausencias de su esposa. Trabaja durante toda el día en el gran comedor de la casa observatorio, al cuál de vez en cuando su cocinero hacía pasar una chuleta (después de su muerte fueron encontrados entremezclados con sus papeles montones de huesos de sus chuletas).
El descubrimiento de Hamilton fue rápidamente seguido por otras nuevas álgebras, tales como las de matrices, que es asimismo no conmutativa. De esta forma comenzó una importante escuela de matemáticas, aunque no había de florecer plenamente hasta después de otros cincuenta años. Recuerdo haber discutido en 1900 con Alfred North Whitehead si los cuaternios y otras álgebras no conmutativas tenían mucho futuro en lo que respecta a las aplicaciones de la física.
Whitehead hizo observar entonces que si bien toda la física hasta entonces conocida podía ser tratada por los métodos del álgebra ordinaria, era posible que pudieran aparecer algún día nuevos campos en la física para los cuales el álgebra no conmutativa sería la única representación natural. En aquel mismo año comenzó el camino hacia la realización de esta conjetura. Max Planck introdujo el cuanto h , el comienzo de la teoría cuántica. Ahora bien, h es un cuanto de acción, y la acción era un concepto central en el sistema central de Hamilton de la dinámica. Así, las ideas de Hamilton sobre dinámica comenzaron a aparecer en primer plano. Pero muy lentamente. Cuando mi libro Dinámica Analítica fue publicado en 1.904, fui criticado severamente por dedicar una gran parte de él a tales temas, como la dualidad entre las coordenadas y el momento, la acción y otras ideas hamiltonianas. Los críticos la llamaron meros juegos matemáticos.
La buena semilla siguió creciendo, sin embargo. El descubrimiento de la relatividad especial trajo los cuaternios al primer plano, porque Arthur Cayley, de la Universidad de Cambridge, había demostrado en 1854 que los cuaternios podían ser aplicados a la representación de rotaciones en un espacio de cuatro dimensiones. Su resultado produjo una expresión particularmente elegante de la transformación más general de Lorentz. Por otra parte los nuevos descubrimientos subrayaron de nuevo la importancia de la acción, que preserva su forma en diferentes sistemas de referencia y es, por tanto, fundamental en la física de la relatividad.
Mientras tanto las investigaciones en la teoría cuántica iban dándose cuenta de que las concepciones dinámicas de Hamilton tenían que constituir la base de todas las reglas de cuantificación. Y en 1925 el otro aspecto de su trabajo, su álgebra no conmutativa, fue introducido en la teoría cuántica por Werner Heisenberg, Max Born y Pascal Jordan, que demostraron que las ecuaciones hamiltonianas de la dinámica eran también válidas en teoría cuántica, supuesto que los símbolos representando las coordenadas y los momentos en la dinámica clásica fueron interpretados como operadores cuyos productos no conmutaban.
El tiempo ha dado la razón ampliamente a la intuición de Hamilton sobre la dualidad entre las coordenadas generalizadas y los momentos generalizados. Esto vino a ser demostrado de una forma sorprendente en 1927, cuando Heisenberg descubrió el principio de la indeterminación, que ordinariamente se enuncia de esta forma: cuando más exactamente son determinadas las coordenadas de una partícula, menos exactamente puede ser conocido su momento, y recíprocamente, siendo el producto de las dos indeterminaciones del orden de la constante de Plank h.
Las investigaciones en mecánica cuántica han tenido la tendencia general ha considerar las matrices más bien que los cuaternios como el tipo de álgebra conmutativa adaptada mejor a sus problemas; pero las formulas originales de Hamilton continúan apareciendo. Así, "las matrices de spin", de Wolfgang Pauli, de las que depende la teoría de las refracciones y momentos angulares de la mecánica cuántica, son simplemente las tres unidades de los cuaternios de Hamilton, i, j, k. Arthur Conway ha demostrado que los métodos de los cuaternios pueden ser usados con ventaja en la discusión de P. A. M. Dirac para el giro del electrón. Las fórmulas de Hamilton de 1843pueden aún resultar ser la expresión más natural de la nueva física.
Principales creaciones intelectuales
Teorema de Hamilton de la hodógrafa. Postula que el vector velocidad de un planeta, sometido a la Ley de Fuerzas de Kepler alrededor del Sol, describe un círculo. Hamilton llamóhodógrafa a la curva descrita por el vector velocidad (del griego hodos, camino).
- Teorema de Cayley-Hamilton
- Ecuación de Hamilton-Jacobi
- Camino hamiltoniano
Publicaciones
- Hamilton, William Rowan (Royal Astronomer Of Ireland), "Introductory Lecture on Astronomy". Dublin University
Review and Quarterly Magazine Vol. I, Trinity College, January 1833.
- Hamilton, William Rowan, "Lectures on Quaternions". Royal Irish Academy, 1853.
Hamilton (1866)Elements of Quaternions University of Dublin Press. Edited by William Edwin Hamilton, son of the deceased author.
- Hamilton (1899)Elements of Quaternions volume I, (1901) volume II. Edited byCharles Jasper Joly; published by Longmans, Green & Co.. David R. Wilkins's collection ofHamilton's Mathematical Papers.