Diferencia entre revisiones de «Secciones cónicas»
m (→Definición) |
|||
| (No se muestran 15 ediciones intermedias de 5 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | |||
{{Definición | {{Definición | ||
|nombre=Secciones cónicas | |nombre=Secciones cónicas | ||
| Línea 5: | Línea 4: | ||
|tamaño= | |tamaño= | ||
|concepto=Toda curva que se obtiene por intersección de un cono y un plano. | |concepto=Toda curva que se obtiene por intersección de un cono y un plano. | ||
| − | }} | + | }} |
| − | |||
| − | |||
| − | |||
| − | Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo | + | '''Secciones cónicas'''. Curva que se obtiene por intersección de un cono y un plano. |
| + | |||
| + | == Historia == | ||
| + | |||
| + | La primera definición conocida de sección cónica surge en la Antigua [[Grecia]], cerca del año 350 (Menæchmus) donde las definieron como [[Corte y sección (dibujo técnico)|secciones]] de un [[Cono]] circular recto. Los nombres de '''Parábola''', '''Elipse''' e '''Hipérbola''' se deben a [[Apolonio de Perge]]. | ||
| + | |||
| + | == Definición == | ||
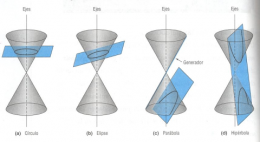
| + | Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene: | ||
| + | # un [[círculo]] | ||
| + | # una [[parábola]] | ||
| + | # una [[elipse]] | ||
| + | # una [[hipérbola]]. | ||
| + | |||
| + | Las cónicas degeneradas (o degradadas) se obtienen si el plano corta al cono en un sólo punto o a lo largo de una o dos rectas situadas en el cono. | ||
| + | |||
| + | La Ecuación General de una sección cónica es: | ||
| + | |||
| + | '''Ax<sup>2</sup> + Bxy + Cy<sup>2</sup> + Dx + Ey + F = 0''' | ||
| + | |||
| + | El tipo de sección puede ser descubierta por el signo de la ecuación siguiente: '''B<sup>2</sup> - 4AC''' | ||
{| cellspacing="1" cellpadding="1" border="1" style="width: 481px; height: 124px;" | {| cellspacing="1" cellpadding="1" border="1" style="width: 481px; height: 124px;" | ||
|- | |- | ||
| − | | Si | + | | valign="middle" align="center" | '''Si B<sup>2</sup> - 4AC es...'''<br> |
| − | | pues la curva es...<br> | + | | valign="middle" align="center" | '''pues la curva es...'''<br> |
|- | |- | ||
| − | | <0<br> | + | | valign="middle" align="center" | <0<br> |
| − | | una elipse, un círculo, un punto o ninguna curva.<br> | + | | valign="middle" align="center" | una [[elipse]], un [[círculo]], un punto o ninguna curva.<br> |
|- | |- | ||
| − | | =0<br> | + | | valign="middle" align="center" | =0<br> |
| − | | una parábola<br> | + | | valign="middle" align="center" | una [[parábola]]<br> |
|- | |- | ||
| − | | >0<br> | + | | valign="middle" align="center" | >0<br> |
| − | | una hipérbola o dos líneas intersectadas<br> | + | | valign="middle" align="center" | una [[hipérbola]] o dos líneas intersectadas<br> |
| − | |} | + | |}{{AP|Excentricidad (matematica)}} |
| + | ==Excentricidad en secciones cónicas== | ||
| + | [[Archivo:Cono y secciones.svg.png|200px|thumb|rigth|Cónicas producidas por secciones al cono]] | ||
| + | *La excentricidad de una [[circunferencia]] es 0 (ε = 0). | ||
| + | *La excentricidad de una [[elipse]] es mayor que cero y menor que 1 (0<ε < 1). | ||
| + | *La excentricidad de una [[parábola]] es 1 (ε = 1). | ||
| + | *La excentricidad de una [[hipérbola]] es mayor que 1 (ε > 1). | ||
| + | |||
| + | == Aplicaciones == | ||
| − | + | Las curvas cónicas son importantes en [[astronomía]]: dos cuerpos masivos que interactúan según la [[ley de gravitación universal]], sus trayectorias describen secciones cónicas si su centro de masa se considera en reposo. Si están relativamente próximas describirán elipses, si se alejan demasiado describirán hipérbolas o parábolas. | |
| − | + | También son importantes en [[aerodinámica]] y en su aplicación industrial, ya que permiten ser repetidas por medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas. | |
| − | |||
| − | También son importantes en aerodinámica y en su aplicación industrial, ya que permiten ser repetidas por medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas. | ||
| − | |||
| − | + | == Fuentes == | |
| − | |||
| − | |||
| − | [[Category:Matemáticas]] | + | *[http://portales.educared.net/wikiEducared/index.php?title=Curvas_c%C3%B3nicas Curvas cónicas] |
| + | *[http://math2.org/math/algebra/es-conics.htm Secciones cónicas] | ||
| + | *[http://es.wikipedia.org/w/index.php?title=Secciones_c%C3%B3nicas Secciones cónicas] | ||
| + | *[http://www.monografias.com/trabajos82/definicion-grandes-conicas/definicion-grandes-conicas.shtml Las grandes cónicas] | ||
| + | * [https://commons.wikimedia.org/wiki/File:Cono_y_secciones.svg Cono y sus secciones] | ||
| + | </div> | ||
| + | [[Category:Matemáticas]][[Categoría:Dibujo]][[Categoría:Dibujo técnico]][[Categoría:Geometría]][[Categoría:Geometría elemental]] | ||
última versión al 16:48 21 abr 2023
| ||||||
Secciones cónicas. Curva que se obtiene por intersección de un cono y un plano.
Historia
La primera definición conocida de sección cónica surge en la Antigua Grecia, cerca del año 350 (Menæchmus) donde las definieron como secciones de un Cono circular recto. Los nombres de Parábola, Elipse e Hipérbola se deben a Apolonio de Perge.
Definición
Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene:
Las cónicas degeneradas (o degradadas) se obtienen si el plano corta al cono en un sólo punto o a lo largo de una o dos rectas situadas en el cono.
La Ecuación General de una sección cónica es:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
El tipo de sección puede ser descubierta por el signo de la ecuación siguiente: B2 - 4AC
| Si B2 - 4AC es... |
pues la curva es... |
| <0 |
una elipse, un círculo, un punto o ninguna curva. |
| =0 |
una parábola |
| >0 |
una hipérbola o dos líneas intersectadas |
Excentricidad en secciones cónicas
- La excentricidad de una circunferencia es 0 (ε = 0).
- La excentricidad de una elipse es mayor que cero y menor que 1 (0<ε < 1).
- La excentricidad de una parábola es 1 (ε = 1).
- La excentricidad de una hipérbola es mayor que 1 (ε > 1).
Aplicaciones
Las curvas cónicas son importantes en astronomía: dos cuerpos masivos que interactúan según la ley de gravitación universal, sus trayectorias describen secciones cónicas si su centro de masa se considera en reposo. Si están relativamente próximas describirán elipses, si se alejan demasiado describirán hipérbolas o parábolas.
También son importantes en aerodinámica y en su aplicación industrial, ya que permiten ser repetidas por medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas.