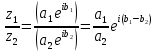Diferencia entre revisiones de «Número complejo»
(→Potenciación) |
(→Veáse también: agregue los numeros naturales fracionarios racionales y enteros) (Etiqueta: revisar proyecto) |
||
| (No se muestran 23 ediciones intermedias de 3 usuarios) | |||
| Línea 5: | Línea 5: | ||
|concepto= | |concepto= | ||
}} | }} | ||
| − | ''' | + | '''Número complejo''' es elemento de un [[Conjunto|conjunto numérico]] surgido para resolver ecuaciones algebraicas que involucren raíz par de un número racional negativo. |
| − | |||
| − | |||
| − | Un | + | == Bases y definición == |
| + | El conjunto de los [[Número real|números reales]], a pesar de su utilidad y universalidad, presenta la gran deficiencia de que: '''no toda ecuación algebraica de grado mayor que 2, con coeficientes enteros, tiene una raíz real'''. Las ecuaciones x<sup>2n</sup> = m, donde n natural y p real negativo no tienen ninguna raíz real. | ||
| + | |||
| + | Un reiterado y notable ejemplo es la ecuación de segundo grado ''x<sup>2</sup> + 1=0'', de donde se obtiene que ''x<sup>2</sup> = -1''. Pero según las reglas del álgebra ningún [[número]] positivo o [[números negativos|negativo]] elevado al cuadrado puede dar -1, es decir no existe ningún [[número]] real ''x'' que satisfaga la ecuación del anterior ejemplo. | ||
La insuficiencia antes planteada ha obligado a los matemáticos a inventar un número ''i'', con la propiedad de que ''i<sup>2</sup> + 1 =0'', la admisión de este número dentro de la gran familia de los [[número]]s ha simplificado considerablemente los cálculos algebraicos. | La insuficiencia antes planteada ha obligado a los matemáticos a inventar un número ''i'', con la propiedad de que ''i<sup>2</sup> + 1 =0'', la admisión de este número dentro de la gran familia de los [[número]]s ha simplificado considerablemente los cálculos algebraicos. | ||
| Línea 23: | Línea 24: | ||
* Representación exponencial. | * Representación exponencial. | ||
| − | ===Representación puntual | + | ===Representación puntual=== |
Se representa el número ''z'' como un punto del plano en coordenadas cartesianas ''(x, y)'', donde ''x'' es la parte real y ''y'' el componente imaginario. | Se representa el número ''z'' como un punto del plano en coordenadas cartesianas ''(x, y)'', donde ''x'' es la parte real y ''y'' el componente imaginario. | ||
Nótese que otras formas de representacion del punto en el plano, como las coordenadas polares no se incluyen en esta forma de representación puntal del número complejo. | Nótese que otras formas de representacion del punto en el plano, como las coordenadas polares no se incluyen en esta forma de representación puntal del número complejo. | ||
| − | ===Representación algebraica | + | ===Representación algebraica=== |
| − | El número complejo ''z'' se representa por una expresión algebraica ''x+yi'', donde ''x'' es la parte real y '' | + | El número complejo ''z'' se representa por una expresión algebraica ''x+yi'', donde ''x'' es la ''parte real '' ; 'y'', la ''parte imaginaria''. |
| − | ===Representación trigonométrica | + | ===Representación trigonométrica=== |
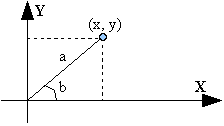
La representación trigonométrica de un número complejo se basa en la representación de un punto por coordenadas polares ''(a, b)'' donde ''a'' es la [[longitud]] del radio vector hasta el punto en cuestión y ''b'' el [[ángulo]] respecto a eje de las ''X''. | La representación trigonométrica de un número complejo se basa en la representación de un punto por coordenadas polares ''(a, b)'' donde ''a'' es la [[longitud]] del radio vector hasta el punto en cuestión y ''b'' el [[ángulo]] respecto a eje de las ''X''. | ||
| Línea 41: | Línea 42: | ||
* [[Archivo:Complejos-julio-b-.gif|middle]] | * [[Archivo:Complejos-julio-b-.gif|middle]] | ||
| − | ===Representación exponencial | + | ===Representación exponencial=== |
La [[Ley de Euler]] para los complejos plantea la asociación: | La [[Ley de Euler]] para los complejos plantea la asociación: | ||
| Línea 104: | Línea 105: | ||
* ''z<sub>3</sub>=z<sub>1</sub>z<sub>2</sub>=(x<sub>1</sub>x<sub>2</sub>-y<sub>1</sub>y<sub>2</sub>)+i(x<sub>1</sub>y<sub>2</sub>+x<sub>2</sub>y<sub>1</sub>)'' | * ''z<sub>3</sub>=z<sub>1</sub>z<sub>2</sub>=(x<sub>1</sub>x<sub>2</sub>-y<sub>1</sub>y<sub>2</sub>)+i(x<sub>1</sub>y<sub>2</sub>+x<sub>2</sub>y<sub>1</sub>)'' | ||
| + | |||
| + | o su versión equivalente en notaciones polares y exponenciales: | ||
| + | |||
| + | * [[Archivo:Numeros_complejos_producto_polar.gif|middle]] | ||
| + | * [[Archivo:Numeros_complejos_producto_exponencial.gif|middle]] | ||
| + | |||
| + | Estas expresiones muestran que el producto de complejos consiste en una rotación y en un cambio de tamaño del módulo del vector resultante. | ||
=== División === | === División === | ||
| − | Para realizar la [[división]] entre números complejos primero debe conocerse la | + | Para realizar la [[división]] entre números complejos primero debe conocerse la conjugada de un número complejo.. |
==== Conjugada ==== | ==== Conjugada ==== | ||
| Línea 127: | Línea 135: | ||
* [[Archivo:Division-numeros-complejos.gif|middle]] | * [[Archivo:Division-numeros-complejos.gif|middle]] | ||
| + | |||
| + | Las notaciones polares y exponenciales son más sencillas e intuitivas para realizar el cociente entre complejos: | ||
| + | |||
| + | * [[Archivo:Numeros_complejos_cociente_polar.gif|middle]] | ||
| + | * [[Archivo:Numeros_complejos_cociente_exponencial.gif|middle]] | ||
| + | |||
| + | Y al igual que en el producto se traduce geométricamente en la rotación y cambio de tamaño del vector resultante. | ||
===Potenciación=== | ===Potenciación=== | ||
| + | Si aceptamos z<sup>r</sup> = e<sup>r(Lnz)</sup>, la potencia de exponente real de un número complejo requiere del logaritmo natural de un número complejo. | ||
| + | |||
| + | Hallar la potencia de base 1 y exponente = raíz cuadrada de 3= 3<sup>1/2</sup>: sea 1<sup>3<sup>1/2</sup></sup>, cuyo resultado es cos(2m 3<sup>1/2</sup> pi) +i sen (2m 3<sup>1/2</sup> pi) donde m es entero cualquiera, pi es el número de Arquímedes = 3.141592... <ref> Volkovyski- Lunts- Aramanovich: ''Problemas sobre la teoría de funciones de variable compleja''. Editorial Mir, Moscú (1972) </ref> | ||
| + | |||
Todo complejo ''z'' puede elevarse a un exponente real ''x'' aplicando la [[Ley de Moivre]]: | Todo complejo ''z'' puede elevarse a un exponente real ''x'' aplicando la [[Ley de Moivre]]: | ||
| Línea 147: | Línea 166: | ||
donde [[Archivo:Coeficiente_binomial.gif|middle]] es el valor del [[coeficiente binomial]] correspondiente a ''n'' y a ''r''. | donde [[Archivo:Coeficiente_binomial.gif|middle]] es el valor del [[coeficiente binomial]] correspondiente a ''n'' y a ''r''. | ||
| − | ==Relación de los complejos con otros conjuntos numéricos | + | ==Relación de los complejos con otros conjuntos numéricos== |
| − | |||
El conjunto de los números complejos es la supérclase de todos los [[Conjunto|conjuntos numéricos]], pues es la unión de los [[Número real|reales]] más los imaginarios. De esa forma quedan incluidas todas las operaciones en este conjunto. | El conjunto de los números complejos es la supérclase de todos los [[Conjunto|conjuntos numéricos]], pues es la unión de los [[Número real|reales]] más los imaginarios. De esa forma quedan incluidas todas las operaciones en este conjunto. | ||
[[Archivo:Jerarquia_conjuntos_numericos.gif]] | [[Archivo:Jerarquia_conjuntos_numericos.gif]] | ||
| − | == Fuentes | + | ==Veáse también== |
| + | * [[Número real]]. | ||
| + | * [[Ley de Euler]]. | ||
| + | * [[Ley de Moivre]]. | ||
| + | * [[Raíz de número complejo]]. | ||
| + | * [[Teorema fundamental del álgebra]]. | ||
| + | *[[Números Naturales]][[Archivo:Logotipo de numeros naturales.png|26px]] | ||
| + | *[[Números racionales]][[Archivo:Logotipo de numeros racionales.png|26px]] | ||
| + | *[[Números enteros]][[Archivo:Logotipo de numeros enteros.png|26px]] | ||
| + | *[[Números fraccionarios]] | ||
| + | |||
| + | ==Referencias == | ||
| + | {{listaref}} | ||
| + | |||
| + | ==Fuentes== | ||
# Michael Spivak. Cálculo infinitesimal. | # Michael Spivak. Cálculo infinitesimal. | ||
# P. E. Danko, A. G. Popov y T. YA. Kozhenikova. Matemática superiores en ejercicios y problemas. | # P. E. Danko, A. G. Popov y T. YA. Kozhenikova. Matemática superiores en ejercicios y problemas. | ||
| + | # A. I. Kostrikin: Introducción al álgebra. Editorial Mir, Moscú (1983), traducido del ruso por Roberto Aníbal Sala; impreso en la URSS. | ||
última versión al 17:22 11 may 2022
| ||||
Número complejo es elemento de un conjunto numérico surgido para resolver ecuaciones algebraicas que involucren raíz par de un número racional negativo.
Sumario
Bases y definición
El conjunto de los números reales, a pesar de su utilidad y universalidad, presenta la gran deficiencia de que: no toda ecuación algebraica de grado mayor que 2, con coeficientes enteros, tiene una raíz real. Las ecuaciones x2n = m, donde n natural y p real negativo no tienen ninguna raíz real.
Un reiterado y notable ejemplo es la ecuación de segundo grado x2 + 1=0, de donde se obtiene que x2 = -1. Pero según las reglas del álgebra ningún número positivo o negativo elevado al cuadrado puede dar -1, es decir no existe ningún número real x que satisfaga la ecuación del anterior ejemplo.
La insuficiencia antes planteada ha obligado a los matemáticos a inventar un número i, con la propiedad de que i2 + 1 =0, la admisión de este número dentro de la gran familia de los números ha simplificado considerablemente los cálculos algebraicos.
Cada número complejo z puede definido como un par ordenado de reales (a,b) donde a es la parte real y b es la parte imaginaria.
Representaciones de números complejos.
Los números complejos tienen varias formas de representación. A saber:
- Representación puntual.
- Representación algebraica.
- Representación trigonométrica.
- Representación exponencial.
Representación puntual
Se representa el número z como un punto del plano en coordenadas cartesianas (x, y), donde x es la parte real y y el componente imaginario.
Nótese que otras formas de representacion del punto en el plano, como las coordenadas polares no se incluyen en esta forma de representación puntal del número complejo.
Representación algebraica
El número complejo z se representa por una expresión algebraica x+yi, donde x es la parte real ; 'y, la parte imaginaria.
Representación trigonométrica
La representación trigonométrica de un número complejo se basa en la representación de un punto por coordenadas polares (a, b) donde a es la longitud del radio vector hasta el punto en cuestión y b el ángulo respecto a eje de las X.
Luego puede representarse al número complejo z = x + yi como z = a cos(b) + a isen(b) donde las representaciones se relacionan de la siguiente manera:
Representación exponencial
La Ley de Euler para los complejos plantea la asociación:
que permite establecer un vínculo entre la representación polar y la exponenciación; de ahí que podamos decir que estamos en presencia de un número complejo normalizado en su forma exponencial:
Donde a y b son los que se definieron en el epígrafe anterior (debe acotarse que b es un ángulo en radianes), mientras k es un entero cualquiera debido a la equivalencia angular tras cada vuelta entera. Si se conoce que c=ln(a), entonces tenemos una representación exponencial del complejp z como sigue:
Aritmética de los números complejos
Los números complejos soportan las operaciones aritméticas elementales:
- Adición.
- Sustracción.
- Multiplicación.
- División.
- Potenciación.
Adición
Sean los números complejos z1 y z2, definidos en notación algebraica como:
- z1=x1+y1i
- z2=x2+y2i
la suma de ambos vendrá dada por el resultado:
- z3=z1+z2=(x1+x2)+i(y1+y2).
Desde el punto de vista de la notación como punto del plano cartesiano, la suma de dos complejos:
(x1,y1)+(x2,y2)
significa un corrimiento a las nuevas coordenadas:
(x1+x2, y1+y2)
Sustracción
Sean los números complejos z1 y z2, definidos en notación algebraica como:
- z1=x1+y1i
- z2=x2+y2i
la resta de ambos vendrá dada por el resultado:
- z3=z1-z2=(x1-x2)+i(y1-y2).
Multiplicación
Sean los números complejos z1 y z2, definidos en notación algebraica como:
- z1=x1+y1i
- z2=x2+y2i
el producto de ambos vendrá dada por el resultado:
z3=z1z2
=(x1+y1i)(x2+y2i)
=x1x2+ix1y2+ix2y1-y1y2
- z3=z1z2=(x1x2-y1y2)+i(x1y2+x2y1)
o su versión equivalente en notaciones polares y exponenciales:
Estas expresiones muestran que el producto de complejos consiste en una rotación y en un cambio de tamaño del módulo del vector resultante.
División
Para realizar la división entre números complejos primero debe conocerse la conjugada de un número complejo..
Conjugada
Sea el número complejo z1:
- z1=x1+y1i
su conjugada viene dado por:
El producto de un complejo por su conjugada es igual a la suma de los cuadrados de las partes real e imaginarias del número complejo en cuestión:
Definición de la operación de división entre números complejos
Sean dos números complejos z1 y z2, la división entre ellos se define por la expresión:
Las notaciones polares y exponenciales son más sencillas e intuitivas para realizar el cociente entre complejos:
Y al igual que en el producto se traduce geométricamente en la rotación y cambio de tamaño del vector resultante.
Potenciación
Si aceptamos zr = er(Lnz), la potencia de exponente real de un número complejo requiere del logaritmo natural de un número complejo.
Hallar la potencia de base 1 y exponente = raíz cuadrada de 3= 31/2: sea 131/2, cuyo resultado es cos(2m 31/2 pi) +i sen (2m 31/2 pi) donde m es entero cualquiera, pi es el número de Arquímedes = 3.141592... [1]
Todo complejo z puede elevarse a un exponente real x aplicando la Ley de Moivre:
que no es sino una aplicación de la potencia a la Ley de Euler:
de manera general, la potencia de un complejo elevado a un real cualquiera en la forma trigonométrica quedaría:
Claro que si estamos en presencia de un natural n podemos aplicar en la forma algebraica la expresión:
donde ![]() es el valor del coeficiente binomial correspondiente a n y a r.
es el valor del coeficiente binomial correspondiente a n y a r.
Relación de los complejos con otros conjuntos numéricos
El conjunto de los números complejos es la supérclase de todos los conjuntos numéricos, pues es la unión de los reales más los imaginarios. De esa forma quedan incluidas todas las operaciones en este conjunto.
Veáse también
- Número real.
- Ley de Euler.
- Ley de Moivre.
- Raíz de número complejo.
- Teorema fundamental del álgebra.
- Números Naturales
- Números racionales
- Números enteros
- Números fraccionarios
Referencias
- ↑ Volkovyski- Lunts- Aramanovich: Problemas sobre la teoría de funciones de variable compleja. Editorial Mir, Moscú (1972)
Fuentes
- Michael Spivak. Cálculo infinitesimal.
- P. E. Danko, A. G. Popov y T. YA. Kozhenikova. Matemática superiores en ejercicios y problemas.
- A. I. Kostrikin: Introducción al álgebra. Editorial Mir, Moscú (1983), traducido del ruso por Roberto Aníbal Sala; impreso en la URSS.