Teorema de los cuatro colores
| ||||
Teorema de los cuatro colores. También teorema de la minimalidad cromática, es un teorema sobre la coloración de grafos que establece que dado cualquier mapa geográfico con regiones continuas, este puede ser coloreado con cuatro colores diferentes, de forma que no queden regiones adyacentes con el mismo color.
Sumario
Historia
En 1852, Francis Guthrie era un estudiante de Augustus De Morgan y formuló este teorema que surgió como una conjetura, que no pudo ser probada por Guthrie, ni por su hermano Frederick, que había sido también estudiante de De Morgan, ni por Sr William Rowan Hamilton, a quien De Morgan le escribió formulando la conjetura.
En 1879 Alfred Bray Kempe anunció en la Revista Nature que tenía una demostración para la conjetura. En 1890, Percy John Heawood encontró un error en la demostración de Kempe. Heawood no pudo demostrar que la conjetura no era válida, pero siguió trabajando en el coloreo de mapas, pudiendo probar que con cinco colores se podía colorear cualquier mapa.
En 1976 la conjetura tuvo demostración, gracias a Kenneth Appel y Wolfgang Haken, que utilizaron un ordenador para la demostración, lo cual generó múltiples controversias en el ambiente matemático.
Formulación precisa del teorema
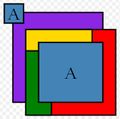
Inicialmente todas las esquinas y puntos en común que pertenecen a tres o más países, deben ser ignoradas. Sin esta restricción, los mapas extraños (utilizando las regiones del área finita pero perímetro infinito) pueden requerir más de cuatro colores. Luego para el propósito del teorema cada país tiene que ser una región simplemente conexa o continua. En el mundo real, esto no es cierto (por ejemplo, Alaska como parte de los Estados Unidos, Nakhchivan como parte de Azerbaiyán, y Kaliningrado como parte de Rusia no son regiones continuas). Debido a que el territorio de un país en particular debe ser del mismo color, si se permitiesen "países" no continuos, cuatro colores podrían no ser suficientes. Por ejemplo:
En este mapa, las dos regiones A pertenecen a un mismo país, y por lo tanto, deben ser del mismo color. En consecuencia, este mapa requiere cinco colores, puesto que las dos regiones A son contiguas con las otras cuatro regiones, y cada una de estas regiones son contiguas entre sí. Si hay tres regiones A, entonces se necesitan seis o más colores; se pueden construir mapas que requieren un número arbitrariamente elevado de colores. Un escenario similar también se puede dar si el color azul se reserva para el agua.
Una versión más simple del teorema utiliza la teoría de grafos. El conjunto de las regiones de un mapa se puede representar de manera más abstracta como un grafo simple no dirigido asociando un vértice para cada región y una arista para cada par de regiones que comparten un segmento de borde. Esta representación del mapa con vértices y aristas es un grafo dual y el problema de colorear países se cambia por la coloración del grafo. Este grafo es plano, o sea, que se puede dibujar en el plano sin cruce de aristas mediante la colocación de cada vértice en un lugar elegido arbitrariamente dentro de la región a la que corresponde. Con la terminología de la teoría de grafos, el teorema de cuatro colores establece que:
Si G es un grafo plano, entonces x(G)<=4.
Resumen de la demostración
Este resumen está basado en el libro Every Planar Map is Four Colorable de Appel y Haken publicado en 1989. Aunque la prueba del teorema de los cuatro colores dada por Kempe contenía un fallo, proporcionó algunas de las herramientas básicas utilizadas posteriormente para demostrarlo. La explicación que se da aquí se ha reformulado utilizando términos modernos de la teoría de grafos.
Kempe argumentó lo siguiente:
Kempe también demostró que G no puede tener ningún vértice de grado 4. Como antes se elimina el vértice v, y cuatro colores de los vértices restantes. Si los cuatro vecinos de V son de diferentes colores, por ejemplo rojo, verde, azul y amarillo en sentido horario, buscamos una ruta alterna de vértices de color rojo y azul que una los vecinos rojo y azul. Tal camino se llama una cadena de Kempe. Puede haber una cadena de Kempe uniendo a los vecinos de color rojo y azul, y puede haber una cadena de Kempe uniendo a los vecinos verdes y amarillos, pero no ambos, ya que estos dos caminos necesariamente se cruzan, y el vértice donde se interceptan no puede ser coloreado. Supongamos que se trata a los vecinos rojos y azules que no están encadenados entre sí. Explora todos los vértices conectados al vecino rojo por el rojo-azul caminos alternos, y luego invertir los colores rojo y azul en todos estos vértices. El resultado sigue siendo un válido de cuatro colores, y ahora V se puede agregar de nuevo y de color rojo.
Bibliografia
- Gonthier, Georges (2008), «Formal Proof--The Four-Color Theorem», Notices of the American Mathematical Society 55 (11): 1382-1393.