Diferencia entre revisiones de «Cicloide»
(→Vea también) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 9 ediciones intermedias de 4 usuarios) | |||
| Línea 1: | Línea 1: | ||
{{Definición | {{Definición | ||
|nombre=Cicloide | |nombre=Cicloide | ||
| − | |imagen= | + | |imagen=Cicloide1.JPG |
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto=Es una curva generada por un punto perteneciente a una circunferencia generatriz al rodar sobre una línea recta directriz, sin deslizarse. |
}} | }} | ||
| − | + | ||
| − | '''Cicloide''' | + | '''Cicloide''', curva plana que es descrita físicamente como la trayectoria de un punto perteneciente a una [[Circunferencia|circunferencia]] generatriz, al rodar sobre una línea recta directriz, sin deslizarse. |
== Historia == | == Historia == | ||
| − | La cicloide ha sido una curva muy estudiada a lo largo de la historia. Ya a finales del siglo XVI, [[Galileo_Galilei|Galileo]] había estudiado esta curva, y fue el primero en darle el nombre con la que la conocemos. Galileo intentó averiguar el | + | La cicloide ha sido una [http://www.disfrutalasmatematicas.com/definiciones/curva.html curva] muy estudiada a lo largo de la historia. Ya a finales del siglo XVI, [[Galileo_Galilei|Galileo]] había estudiado esta curva, y fue el primero en darle el nombre con la que la conocemos. Galileo intentó averiguar el Segmentoárea]] de esta curva sumando diferentes [[Segmento|segmentos]] rectos situados sobre la misma, mediante aproximación. |
| − | Uno de los primeros que consiguieron resultados sobre la cicloide fue [http:// | + | Uno de los primeros que consiguieron resultados sobre la cicloide fue [http://www.biografiasyvidas.com/biografia/.../roberval.htm Gilles de Roberval], demostró que el [[Área|área]] encerrada por un [http://www.disfrutalasmatematicas.com/definiciones/arco.html arco] de cicloide es exactamente tres veces el área de la circunferencia que la genera. Más adelante también encontró un método para trazar la [[Tangente|tangente]] a la cicloide un punto cualquiera de la misma (problema resuelto también por [[Pierre_de_Fermat|Fermat]] y [[Descartes]]) y realizó cálculo relacionados con [[Cuerpos_geométricos_(Volumen)|volúmenes]] de revolución asociados a la cicloide. |
[[Evangelista_Torricelli|Torricelli]] publicó sus soluciones a varias de las cuestiones resueltas por Roberval. | [[Evangelista_Torricelli|Torricelli]] publicó sus soluciones a varias de las cuestiones resueltas por Roberval. | ||
| − | En [[1658]] [ | + | En [[1658]] [[Christopher Wren]] calculó que la longitud de un arco de cicloide es cuatro veces el diámetro de la circunferencia que genera dicha curva. |
| − | En [[1696]] el matemático [[Johann_Bernoulli|Johann Bernoulli]] anunció a la comunidad matemática la solución al problema de la [http:// | + | En [[1696]] el matemático [[Johann_Bernoulli|Johann Bernoulli]] anunció a la comunidad matemática la solución al problema de la [http://www.principia-malaga.com/portal/pdfs/web-braquistocrona.pdf| braquistocrona] (curva que sigue el descenso más rápido cuando existe [[Gravedad|gravedad]] y que es objeto de estudio en el cálculo de variaciones), mostrando que la solución era una cicloide. |
== Ecuaciones == | == Ecuaciones == | ||
| Línea 28: | Línea 28: | ||
y = a(1-cost)</big> | y = a(1-cost)</big> | ||
| − | t es un parámetro real. Siendo la variable y función de la [[Variables|variable]] x, esta cicloide tiene un período de 2aπ, y una altura de 2a. | + | t es un parámetro real. Siendo la variable y [[Función|función]] de la [[Variables|variable]] x, esta cicloide tiene un período de 2aπ, y una altura de 2a. |
| − | * Si se despeja la variable t en la ecuación paramétrica, se obtendrá la forma cartesiana: | + | * Si se despeja la variable t en la [http://es.wikipedia.org/wiki/Ecuaci%C3%B3n_param%C3%A9trica ecuación paramétrica], se obtendrá la forma [http://es.wikipedia.org/wiki/Coordenadas_cartesianas cartesiana]: |
[[Image:Ecuac_cicloide.png]] | [[Image:Ecuac_cicloide.png]] | ||
| − | El único parámetro de forma es el radio a de la circunferencia generatriz. Esta fórmula es válida para la variable y en el intervalo [0,2a], y proporciona sólo la mitad del primer bucle de la cicloide. | + | El único parámetro de forma es el [http://www.disfrutalasmatematicas.com/definiciones/radio.html radio] a de la circunferencia generatriz. Esta fórmula es válida para la variable y en el intervalo [0,2a], y proporciona sólo la mitad del primer bucle de la cicloide. |
* La ecuación en forma intrínseca es: | * La ecuación en forma intrínseca es: | ||
| Línea 48: | Línea 48: | ||
=== Propiedad geométrica === | === Propiedad geométrica === | ||
| − | La propiedad de la evoluta o envolvente del haz las normales | + | La propiedad de la [http://es.wikipedia.org/wiki/Evoluta evoluta] o envolvente del haz las normales |
=== Propiedades físicas === | === Propiedades físicas === | ||
| − | + | Las propiedades [[Física|físicas]] que han contribuido grandemente a la fama de esta curva son: | |
| − | |||
| − | |||
| − | + | # [http://www.planetamatematico.com/index.php? Tautocronía]] | |
| + | # [http://www.principia-malaga.com/portal/pdfs/web-braquistocrona.pdf Braquistocronía] | ||
== Aplicaciones == | == Aplicaciones == | ||
| − | En el diseño de los dientes de los engranajes se emplean curvas cicloides (así lo propuso [http:// | + | En el diseño de los dientes de los [http://es.wikipedia.org/wiki/Engranaje engranajes] se emplean curvas cicloides (así lo propuso [http://www.biografiasyvidas.com/.../d/desargues.htm Gérard Desargues] en el año [[1630]]). |
| − | En Física se puede ver que un [[Péndulo|péndulo]] que tenga por límites una curva cicloide es isócrono y el centro de gravedad del péndulo describe a su vez una cicloide. | + | En Física se puede ver que un [[Péndulo|péndulo]] que tenga por límites una curva cicloide es [http://www.wordreference.com/definicion/is%C3%B3crono isócrono] y el centro de gravedad del péndulo describe a su vez una cicloide. |
| − | Un uso practico es el diseño de ciertos | + | Un uso practico es el diseño de ciertos toboganes. Los hechos con forma de cicloide se utilizaron en la industria aeronaútica, pues se requería una forma apropiada de salir deslizándose desde un [[Avion|avión]] en caso de emergencia. |
| − | == | + | == Veáse también == |
*[[Parábola|Parábola]] | *[[Parábola|Parábola]] | ||
| Línea 84: | Línea 83: | ||
*[[Folium de Descartes|Folium de Descartes]] | *[[Folium de Descartes|Folium de Descartes]] | ||
| − | *[[ | + | *[[Hipocicloide|Hipocicloide]] |
| − | + | *[[Cardioide|Cardioide]] | |
| − | * | + | == Enlaces externos == |
| + | *[http://es.wikipedia.org/wiki/Generatriz Generatriz] | ||
| + | *[http://es.wikipedia.org/wiki/Directriz directriz] | ||
| + | *[http://es.wikipedia.org/wiki/Tobog%C3%A1n Toboganes] | ||
| + | *[http://enciclopedia.us.es/index.php/Industria_aeron%C3%A1utica Industria aeronaútica] | ||
| + | *[http://es.wikipedia.org/wiki/G%C3%A9rard_Desargues Gérard Desargues] | ||
| + | *[http://gaussianos.com/la-cicloide-%C2%BFcual-es-el-camino-mas-corto Tautocronía] | ||
| + | *[http://es.wikipedia.org/wiki/Curva_braquist%C3%B3crona Braquistocronía] | ||
| + | *[http://es.wikipedia.org/wiki/Christopher_Wren Christopher Wren] | ||
| + | *[http://en.wikipedia.org/wiki/Gilles_de_Roberval Roberval] | ||
| − | * | + | == Fuentes == |
| + | * [http://www.es.wikipedia.org/wiki/Cicloide Cicloide]. | ||
| + | * [http://www.gaussianos.com/la-cicloide-%C2%BFcual-es-el-camino-mas-corto/Gaussianos/ La cicloide] | ||
[[Category:Matemáticas]][[Category:Geometría]] | [[Category:Matemáticas]][[Category:Geometría]] | ||
última versión al 16:48 31 jul 2019
| ||||||
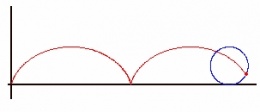
Cicloide, curva plana que es descrita físicamente como la trayectoria de un punto perteneciente a una circunferencia generatriz, al rodar sobre una línea recta directriz, sin deslizarse.
Sumario
Historia
La cicloide ha sido una curva muy estudiada a lo largo de la historia. Ya a finales del siglo XVI, Galileo había estudiado esta curva, y fue el primero en darle el nombre con la que la conocemos. Galileo intentó averiguar el Segmentoárea]] de esta curva sumando diferentes segmentos rectos situados sobre la misma, mediante aproximación.
Uno de los primeros que consiguieron resultados sobre la cicloide fue Gilles de Roberval, demostró que el área encerrada por un arco de cicloide es exactamente tres veces el área de la circunferencia que la genera. Más adelante también encontró un método para trazar la tangente a la cicloide un punto cualquiera de la misma (problema resuelto también por Fermat y Descartes) y realizó cálculo relacionados con volúmenes de revolución asociados a la cicloide.
Torricelli publicó sus soluciones a varias de las cuestiones resueltas por Roberval.
En 1658 Christopher Wren calculó que la longitud de un arco de cicloide es cuatro veces el diámetro de la circunferencia que genera dicha curva.
En 1696 el matemático Johann Bernoulli anunció a la comunidad matemática la solución al problema de la braquistocrona (curva que sigue el descenso más rápido cuando existe gravedad y que es objeto de estudio en el cálculo de variaciones), mostrando que la solución era una cicloide.
Ecuaciones
- Ecuación paramétrica:
x = a(t-sent)
y = a(1-cost)
t es un parámetro real. Siendo la variable y función de la variable x, esta cicloide tiene un período de 2aπ, y una altura de 2a.
- Si se despeja la variable t en la ecuación paramétrica, se obtendrá la forma cartesiana:
El único parámetro de forma es el radio a de la circunferencia generatriz. Esta fórmula es válida para la variable y en el intervalo [0,2a], y proporciona sólo la mitad del primer bucle de la cicloide.
- La ecuación en forma intrínseca es:
ρ2 + s2 = 16 a2
Donde igualmente ρ representa el radio de la curva es la abscisa curvilínea.
Propiedades
La Cicloide presenta algunas propiedades que no se encuentran en la generalidad de las curvas planas.
Propiedad geométrica
La propiedad de la evoluta o envolvente del haz las normales
Propiedades físicas
Las propiedades físicas que han contribuido grandemente a la fama de esta curva son:
Aplicaciones
En el diseño de los dientes de los engranajes se emplean curvas cicloides (así lo propuso Gérard Desargues en el año 1630).
En Física se puede ver que un péndulo que tenga por límites una curva cicloide es isócrono y el centro de gravedad del péndulo describe a su vez una cicloide.
Un uso practico es el diseño de ciertos toboganes. Los hechos con forma de cicloide se utilizaron en la industria aeronaútica, pues se requería una forma apropiada de salir deslizándose desde un avión en caso de emergencia.
Veáse también
Enlaces externos
- Generatriz
- directriz
- Toboganes
- Industria aeronaútica
- Gérard Desargues
- Tautocronía
- Braquistocronía
- Christopher Wren
- Roberval