Diferencia entre revisiones de «Número e»
(Página creada con '{{Definición|nombre=Número e|imagen=E.png|concepto= ''e=2,718 281 828 459...''}} <div align=> '''Número ''e'' '''. Número irracional y [[Número trascendental|trascenden...') |
(→Definiciones: sale) |
||
| (No se muestran 21 ediciones intermedias de 6 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | {{Definición|nombre=Número e|imagen= | + | {{Definición |
| − | <div align=> | + | |nombre=Número e |
| − | '''Número ''e'' '''. [[ | + | |imagen=Constante_e.png |
| + | |concepto= Límite de una sucesión monótona: ''e''=2,718 281 828 459... | ||
| + | }} | ||
| + | <div align=justify> | ||
| + | '''Número ''e'' '''. Es uno de los números reales más importantes al lado de 0, 1 y pi. Obtenido por un nuevo recurso de la matemática del movimiento: límite de una sucesión. Es [[Números irracionales|número irracional]] y [[Número trascendental|trascendente]], base del sistema de los [[logaritmo|logaritmos naturales o neperianos]], cuya primera referencia se debe al matemático y teólogo escocés [[John Napier]] en su trabajo ''Mirifici Logarithmorum Canonis Descriptio'' de [[1614]], aunque en el mismo no aparecía aproximación alguna del valor numérico de ''e'' hasta que [[Jacob Bernoulli]] obtuvo el primer valor resolviendo un problema de interés compuesto sobre una cantidad inicial fija con variación continua del tiempo. | ||
| − | + | Las funciones que parten de su valor: el logaritmo natural y la [[función exponencial]] tienen propiedades bien conocidas dentro de las [[matemática|matemáticas]] y expresiones simples de [[cálculo numérico]] que permite que sobre ellas se soporten computacionalmente otras funciones tradicionales. Por ejemplo, los valores menos típicos del [[seno]] y [[coseno]] se calculan aprovenchando la relación entre las representaciones trigonométrica y exponencial de los [[Número complejo|números complejos]]. | |
| − | |||
| − | Las funciones que parten de su valor: el logaritmo natural y la [[función exponencial]] tienen propiedades bien conocidas dentro de las matemáticas y expresiones simples de cálculo numérico que permite que sobre ellas se soporten computacionalmente otras funciones tradicionales. Por ejemplo, los valores menos típicos del [[seno]] y [[coseno]] se calculan aprovenchando la relación entre las representaciones trigonométrica y exponencial de los [[Número complejo|números complejos]]. | ||
| + | ==Nombres equivalentes== | ||
Entre sus muchos nombres equivalentes están: | Entre sus muchos nombres equivalentes están: | ||
* Constante ''e''. | * Constante ''e''. | ||
* Número o constante de [[Euler]]. | * Número o constante de [[Euler]]. | ||
| − | * Número o constante de Napier (o | + | * Número o constante de Napier (o Neper, como suele latinizarse). |
| − | ==Historia | + | ==Historia== |
La primera referencia indirecta a ''e'' está dada en ''Mirifici Logarithmorum Canonis Descriptio'', el famoso texto de 1614 de John Napier donde se exponía por primera vez sus ideas sobre logaritmos, antilogaritmos, resultados y tablas de cálculos de los mismos; sin embargo la primera aproximación la obtendría Jacob Bernoulli en la solución del problema del interés a largo plazo de una cantidad fija inicial que lo llevó tras sucesivas iteraciones al muy conocido ahora límite: | La primera referencia indirecta a ''e'' está dada en ''Mirifici Logarithmorum Canonis Descriptio'', el famoso texto de 1614 de John Napier donde se exponía por primera vez sus ideas sobre logaritmos, antilogaritmos, resultados y tablas de cálculos de los mismos; sin embargo la primera aproximación la obtendría Jacob Bernoulli en la solución del problema del interés a largo plazo de una cantidad fija inicial que lo llevó tras sucesivas iteraciones al muy conocido ahora límite: | ||
| + | [[Archivo:Limite_fundamental_algebraico_natural.gif|middle]] | ||
| + | |||
| + | cuyo valor fijó en ''2.7182818''. | ||
| + | Luego el [[matemático]] y [[filósofo]] [[Gottfried Leibniz]] en las cartas de [[1690]] y [[1691]] a [[Christiaan Huygens]] hizo uso del valor representándolo con la letra ''b''. | ||
| + | Fue Leonard Euler quien comenzó en 1727 a identificar el número con su símbolo actual: la letra ''e'', pero no es hasta diez años después que la presenta a la comunidad matemática en su libro ''Mechanica''. | ||
| − | [[ | + | Posteriormente los especialistas usarían ''a'', ''b'', ''c'' y ''e'', hasta que finalmente triunfó esta última para representar al número irracional. |
| + | [[Charles Hermite]] demostró en [[1873]] que se trataba de un número trascendental. | ||
| + | Sus aproximaciones comenzaron con el trabajo de Bernoulli, después Euler realizó una aproximación de 18 lugares tras la coma y así se han producido al igual que en la determinación de los lugares de ''pi'' una especie de carrera que tuvo en [[2010]] su más reciente edición cuando Shigeru Kondo y Alexander J. Yee determinaron 1 billón de decimales exactos de ''e''. | ||
| + | |||
| + | ==Definiciones== | ||
| + | * El número de Euler, junto con el número pi de Arquímedes ocupa un lugar señero en la matemática, desde la aparición en 1748 de la obra ''Introductio in Analyssin Infinotorum'' de Euler. Depara un magnífico método en que el principio de las sucesiones monótonas puede ser usado para definir un nuevo número real. Usando la notación | ||
| − | + | ::::n!=1·2.3.4...n | |
| − | + | para los primeros n enteros positivos, sea la sucesión a<sub>1</sub>, a<sub>2</sub>, a<sub>3</sub> en la cual | |
| − | + | :::. a<sub>n</sub> = 1+1/1! + 1/2! + ... +1/n! | |
| − | + | Los términos a<sub>n</sub> forman una sucesión creciente, pues el siguiente se obtiene sumando un valor positivo 1/(i+1)! Además están acotados superiormente a<sub>n</sub> < C = 3, lo que se prueba comparando con una progresión geométrica de razón 1/2. | |
| − | + | Según el principio de las sucesiones monótonas, cuando n tiende a ∞, a<sub>n</sub> debe acercarse a un límite, y a este ''límite llamaremos e''. Para denotar ''e''=lim a<sub>n</sub>, se puede escribir ''e'' en forma de serie | |
| − | + | :::::e = 1+1/1! + 1/2! + ... +1/n!+... <ref>Courant/ Robbins : "¿Qué es la matemática?", Aguilar S. A. Madrid, 1979 </ref> | |
| − | |||
El número real ''e'' es el resultado de las siguientes expresiones: | El número real ''e'' es el resultado de las siguientes expresiones: | ||
# [[Archivo:Limite_fundamental_algebraico.gif|middle]] ([[Límite fundamental algebraico]]). | # [[Archivo:Limite_fundamental_algebraico.gif|middle]] ([[Límite fundamental algebraico]]). | ||
| − | |||
# Las fracciones continuas: | # Las fracciones continuas: | ||
## [[Archivo:Fraccion_continua_normalizada_de_e.gif|middle]] (descubierta por Leonard Euler). | ## [[Archivo:Fraccion_continua_normalizada_de_e.gif|middle]] (descubierta por Leonard Euler). | ||
| Línea 38: | Línea 49: | ||
# ''ln x = 1''. | # ''ln x = 1''. | ||
| − | ==Importancia | + | ==Importancia== |
| − | La constante de Euler tiene una serie de propiedades | + | La constante de Euler es de radical importancia primero en las [[matemáticas]] y luego en muchos otros sectores de la producción, la [[ciencia]] y la vida cotidiana. Si bien el [[número pi]] es importante en el predio de la [[trigonometría]] circular; ''e'' juega un papel primordial en el [[cálculo|análisis]], en tanto forma parte de muchos de los resultados fundamentales de [[Límite matemático|límites]], [[Derivada|derivadas]], [[Integral|integrales]], ecuaciones diferenciales, trigonometría hiperbólica, series, etc. |
| + | Esta constante tiene una serie de propiedades que permiten su empleo en la definición de expresiones de gran aplicación en muchas áreas del conocimiento humano: la campana de Gauss. | ||
Primeramente, ''e'' es un número irracional cuya demostración se realiza mediante el ''método de reducción al absurdo''. Charles Hermite demostró que es un número trascendente y se plantea que es [[Número normal|normal]]. | Primeramente, ''e'' es un número irracional cuya demostración se realiza mediante el ''método de reducción al absurdo''. Charles Hermite demostró que es un número trascendente y se plantea que es [[Número normal|normal]]. | ||
Luego, su valor constituye el resultado del límite fundamental algebraico: | Luego, su valor constituye el resultado del límite fundamental algebraico: | ||
| − | + | ||
* [[Archivo:Limite_fundamental_algebraico.gif|middle]] | * [[Archivo:Limite_fundamental_algebraico.gif|middle]] | ||
| − | + | ||
Es la base de la función logaritmo natural definida: | Es la base de la función logaritmo natural definida: | ||
| − | + | ||
| − | * [[Archivo:Ln_definicion|middle]]. | + | * [[Archivo:Ln_definicion.gif|middle]]. |
| − | + | ||
| + | La misma posee la siguiente descomposición en series de potencia según Taylor: | ||
| + | |||
| + | * [[Archivo:Ln_desarrollo_Lagrange.gif|middle]] para ''x>0'' | ||
| + | |||
| + | Lo que la hace una candidata potencial para el cálculo de otros logaritmos en vista de la propiedad fundamental del logaritmo: | ||
| + | |||
| + | * [[Archivo:Log_a_x_igual_ln_x.gif|middle]] | ||
| + | |||
la cual es la [[función inversa]] de la exponencial: | la cual es la [[función inversa]] de la exponencial: | ||
| − | + | ||
* [[Archivo:Funcion_Exponencial_definicion.gif|middle]] | * [[Archivo:Funcion_Exponencial_definicion.gif|middle]] | ||
| − | + | ||
| − | que como se conoce conserva su propiedad ante la integral y la derivada es decir: | + | que como se conoce conserva su propiedad ante la integral y la derivada, es decir: |
| − | + | ||
* [[Archivo:Derivada_exponencial.gif|middle]] | * [[Archivo:Derivada_exponencial.gif|middle]] | ||
* [[Archivo:Integral_exponencial.gif|middle]] | * [[Archivo:Integral_exponencial.gif|middle]] | ||
| − | + | ||
| − | quien puede calcularse computacionalmente por ejemplo mediante el desarrollo de series de derivadas de | + | quien puede calcularse computacionalmente, por ejemplo, mediante el desarrollo de series de derivadas de Taylor: |
| − | + | ||
* [[Archivo:Exponencial_desarrollo_Lagrange.gif|middle]] (1) | * [[Archivo:Exponencial_desarrollo_Lagrange.gif|middle]] (1) | ||
| + | |||
| + | Este desarrollo es muy ventajoso para el cálculo computacional y por ende, de exponenciaciones en otras bases a partir de la transformación solo en función de ''e<sup>x</sup>'' y ''ln(x)'': | ||
| + | |||
| + | * ''a<sup>x</sup>=e<sup>x</sup>'' | ||
| + | |||
| + | La función exponencial puede expandirse al [[cuerpo algebraico|cuerpo]] de los números complejos gracias a la relación entre las representaciones exponencial y trigonométrica de aquellos. | ||
| + | |||
| + | * [[Archivo:Numero_complejo_representacion_exponencial.gif|middle]] | ||
| + | |||
| + | y ya que el argumento [[Archivo:Theta.gif|middle]] es un real (ángulo en radianes) cualquiera esto permite obtener versiones de (1) como: | ||
| + | |||
| + | * [[Archivo:Desarrollo_intermedio_calculo_seno_coseno.gif|middle]] | ||
| + | |||
| + | que una vez desarrolladas las potencias y agrupadas las partes reales e imaginarias como cosenos y senos, respectivamente, quedan expresados: | ||
| + | |||
| + | * [[Archivo:Seno_igual_parte_imaginaria_exp_ix.gif|middle]] o mejor [[Archivo:Seno_desarrollo_Lagrange.gif|middle]] | ||
| + | * [[Archivo:Coseno_igual_parte_real_exp_ix.gif|middle]] o [[Archivo:Coseno_desarrollo_Lagrange.gif|middle]] | ||
| + | |||
| + | La definición de las funciones hiperbólicas ''senh'' y ''cosh'' pueden describirse fácilmente mediante la relación: | ||
| + | |||
| + | * ''e<sup>x</sup>=senh(x)+cosh(x)'' | ||
| + | |||
| + | puesto que: | ||
| + | |||
| + | * [[Archivo:Definicion_exponencial_senh.gif|middle]] | ||
| + | * [[Archivo:Definicion_exponencial_cosh.gif|middle]] | ||
| + | * [[Archivo:Definicion_exponencial_tanh.gif|middle]] | ||
| + | |||
| + | También tiene uso en la modelación de fenómenos de las [[finanzas]] y la [[economía]], el comportamiento del crecimiento de poblaciones de especies biológicas, el tiempo medio de desintegración de [[Isótopo|isótopos]] y [[Partícula subatómica|partículas subatómicas]], modelos climáticos, etc. | ||
| − | y | + | ==Presencia y peculiaridades== |
| + | # Sirve como base del sistema de logaritmos neperianos o naturales; se denota por lnx = t, donde x es un número real positivo y t es positivo para x>1 y negativo para x <1. ln 1 = 0.La equivalencia es lnx = t si, solo si x = e<sup>t</sup> . | ||
| + | # Se hace presente en la definición de la función y(x) = e<sup>x</sup>, o bien y(x) = exp(x), siendo su conjunto de valores admisibles CVA el conjunto R de todos los números reales. | ||
| + | # Al definir un número complejo de módulo 1, se tiene la expresión e <sup>{ix}</sup> = cosx + isenx . Geométricamente representa una circunferencia de radio1, centro: O | ||
| + | # De lo anterior resulta e<sup> iπ</sup> + 1 = 0 | ||
| − | + | ===Caraterísticas=== | |
| + | # e es un número real irracional, esto es, que no puede expresar como la razón de dos números enteros; pues no es un número racional.. | ||
| + | # e es un número trascendente, lo que significa que no puede ser raíz de una ecuación algebraica, de aquellas que tienen coeficientes racionales. | ||
| + | # Se presenta en la solución de ecuaciones diferenciales ordinarias, entre otras, del tipo dx/dt = kx | ||
| + | #Su desarrollo polinómico sirve para definir la exponencial de una matriz, usada en la solución de un sistema de ecuaciones diferenciales ordinarias. <ref> Piskunov: ''Cálculo diferencial e integral'' tomo I. Editorial Mir, Moscú (1983) sexta edición</ref>. | ||
| − | ==Fuentes | + | ==Fuentes== |
| − | + | * Allendoerfer, Carl B., Cletus O. Oakley. Introducción moderna a la matemática superior. [[Ediciones del Castillo]], [[Madrid]]. [[1967]]. | |
| − | + | * Ríbnikov, K. Historia de las matemáticas. [[Editorial MIR]], [[Moscú]]. [[1987]]. | |
| − | + | * Artículo: [http://es.wikipedia.org/wiki/Número_e Número e en Wikipedia]. Disponible en: "es.wikipedia.org". Consultado: 27 de febrero de 2012. | |
| − | </ | + | ==Referencias y notas== |
| − | [[Categoría:Matemáticas]] | + | <references/> |
| + | [[Categoría:Matemáticas]][[Categoría:Análisis matemático]][[Categoría:Constantes matemáticas]][[Categoría:Base de logaritmos]] | ||
última versión al 00:13 12 ene 2020
| ||||||
Número e . Es uno de los números reales más importantes al lado de 0, 1 y pi. Obtenido por un nuevo recurso de la matemática del movimiento: límite de una sucesión. Es número irracional y trascendente, base del sistema de los logaritmos naturales o neperianos, cuya primera referencia se debe al matemático y teólogo escocés John Napier en su trabajo Mirifici Logarithmorum Canonis Descriptio de 1614, aunque en el mismo no aparecía aproximación alguna del valor numérico de e hasta que Jacob Bernoulli obtuvo el primer valor resolviendo un problema de interés compuesto sobre una cantidad inicial fija con variación continua del tiempo.
Las funciones que parten de su valor: el logaritmo natural y la función exponencial tienen propiedades bien conocidas dentro de las matemáticas y expresiones simples de cálculo numérico que permite que sobre ellas se soporten computacionalmente otras funciones tradicionales. Por ejemplo, los valores menos típicos del seno y coseno se calculan aprovenchando la relación entre las representaciones trigonométrica y exponencial de los números complejos.
Sumario
Nombres equivalentes
Entre sus muchos nombres equivalentes están:
- Constante e.
- Número o constante de Euler.
- Número o constante de Napier (o Neper, como suele latinizarse).
Historia
La primera referencia indirecta a e está dada en Mirifici Logarithmorum Canonis Descriptio, el famoso texto de 1614 de John Napier donde se exponía por primera vez sus ideas sobre logaritmos, antilogaritmos, resultados y tablas de cálculos de los mismos; sin embargo la primera aproximación la obtendría Jacob Bernoulli en la solución del problema del interés a largo plazo de una cantidad fija inicial que lo llevó tras sucesivas iteraciones al muy conocido ahora límite:
![]()
cuyo valor fijó en 2.7182818. Luego el matemático y filósofo Gottfried Leibniz en las cartas de 1690 y 1691 a Christiaan Huygens hizo uso del valor representándolo con la letra b. Fue Leonard Euler quien comenzó en 1727 a identificar el número con su símbolo actual: la letra e, pero no es hasta diez años después que la presenta a la comunidad matemática en su libro Mechanica.
Posteriormente los especialistas usarían a, b, c y e, hasta que finalmente triunfó esta última para representar al número irracional. Charles Hermite demostró en 1873 que se trataba de un número trascendental. Sus aproximaciones comenzaron con el trabajo de Bernoulli, después Euler realizó una aproximación de 18 lugares tras la coma y así se han producido al igual que en la determinación de los lugares de pi una especie de carrera que tuvo en 2010 su más reciente edición cuando Shigeru Kondo y Alexander J. Yee determinaron 1 billón de decimales exactos de e.
Definiciones
- El número de Euler, junto con el número pi de Arquímedes ocupa un lugar señero en la matemática, desde la aparición en 1748 de la obra Introductio in Analyssin Infinotorum de Euler. Depara un magnífico método en que el principio de las sucesiones monótonas puede ser usado para definir un nuevo número real. Usando la notación
- n!=1·2.3.4...n
para los primeros n enteros positivos, sea la sucesión a1, a2, a3 en la cual
- . an = 1+1/1! + 1/2! + ... +1/n!
Los términos an forman una sucesión creciente, pues el siguiente se obtiene sumando un valor positivo 1/(i+1)! Además están acotados superiormente an < C = 3, lo que se prueba comparando con una progresión geométrica de razón 1/2.
Según el principio de las sucesiones monótonas, cuando n tiende a ∞, an debe acercarse a un límite, y a este límite llamaremos e. Para denotar e=lim an, se puede escribir e en forma de serie
- e = 1+1/1! + 1/2! + ... +1/n!+... [1]
El número real e es el resultado de las siguientes expresiones:
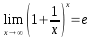 (Límite fundamental algebraico).
(Límite fundamental algebraico).- Las fracciones continuas:
- ln x = 1.
Importancia
La constante de Euler es de radical importancia primero en las matemáticas y luego en muchos otros sectores de la producción, la ciencia y la vida cotidiana. Si bien el número pi es importante en el predio de la trigonometría circular; e juega un papel primordial en el análisis, en tanto forma parte de muchos de los resultados fundamentales de límites, derivadas, integrales, ecuaciones diferenciales, trigonometría hiperbólica, series, etc. Esta constante tiene una serie de propiedades que permiten su empleo en la definición de expresiones de gran aplicación en muchas áreas del conocimiento humano: la campana de Gauss.
Primeramente, e es un número irracional cuya demostración se realiza mediante el método de reducción al absurdo. Charles Hermite demostró que es un número trascendente y se plantea que es normal.
Luego, su valor constituye el resultado del límite fundamental algebraico:
Es la base de la función logaritmo natural definida:
La misma posee la siguiente descomposición en series de potencia según Taylor:
Lo que la hace una candidata potencial para el cálculo de otros logaritmos en vista de la propiedad fundamental del logaritmo:
la cual es la función inversa de la exponencial:
que como se conoce conserva su propiedad ante la integral y la derivada, es decir:
quien puede calcularse computacionalmente, por ejemplo, mediante el desarrollo de series de derivadas de Taylor:
Este desarrollo es muy ventajoso para el cálculo computacional y por ende, de exponenciaciones en otras bases a partir de la transformación solo en función de ex y ln(x):
- ax=ex
La función exponencial puede expandirse al cuerpo de los números complejos gracias a la relación entre las representaciones exponencial y trigonométrica de aquellos.
y ya que el argumento ![]() es un real (ángulo en radianes) cualquiera esto permite obtener versiones de (1) como:
es un real (ángulo en radianes) cualquiera esto permite obtener versiones de (1) como:
que una vez desarrolladas las potencias y agrupadas las partes reales e imaginarias como cosenos y senos, respectivamente, quedan expresados:
La definición de las funciones hiperbólicas senh y cosh pueden describirse fácilmente mediante la relación:
- ex=senh(x)+cosh(x)
puesto que:
También tiene uso en la modelación de fenómenos de las finanzas y la economía, el comportamiento del crecimiento de poblaciones de especies biológicas, el tiempo medio de desintegración de isótopos y partículas subatómicas, modelos climáticos, etc.
Presencia y peculiaridades
- Sirve como base del sistema de logaritmos neperianos o naturales; se denota por lnx = t, donde x es un número real positivo y t es positivo para x>1 y negativo para x <1. ln 1 = 0.La equivalencia es lnx = t si, solo si x = et .
- Se hace presente en la definición de la función y(x) = ex, o bien y(x) = exp(x), siendo su conjunto de valores admisibles CVA el conjunto R de todos los números reales.
- Al definir un número complejo de módulo 1, se tiene la expresión e {ix} = cosx + isenx . Geométricamente representa una circunferencia de radio1, centro: O
- De lo anterior resulta e iπ + 1 = 0
Caraterísticas
- e es un número real irracional, esto es, que no puede expresar como la razón de dos números enteros; pues no es un número racional..
- e es un número trascendente, lo que significa que no puede ser raíz de una ecuación algebraica, de aquellas que tienen coeficientes racionales.
- Se presenta en la solución de ecuaciones diferenciales ordinarias, entre otras, del tipo dx/dt = kx
- Su desarrollo polinómico sirve para definir la exponencial de una matriz, usada en la solución de un sistema de ecuaciones diferenciales ordinarias. [2].
Fuentes
- Allendoerfer, Carl B., Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
- Ríbnikov, K. Historia de las matemáticas. Editorial MIR, Moscú. 1987.
- Artículo: Número e en Wikipedia. Disponible en: "es.wikipedia.org". Consultado: 27 de febrero de 2012.


