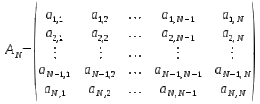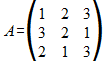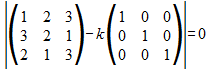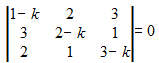Diferencia entre revisiones de «Polinomio característico»
(Página creada con «{{Definición|Nombre=Polinomio característico|imagen=MatrizCuadradaOrdenN.gif|concepto=Polinomio de grado ''N'' derivado de ''|A-xI|=0'' donde ''A'' es una matriz as...») |
(→Fuentes: Hay varios libros de álgebra lineal de la Editorial Mir) |
||
| (No se muestran 8 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | {{Definición|Nombre=Polinomio característico|imagen=MatrizCuadradaOrdenN.gif|concepto=[[Polinomio]] de grado ''N'' derivado de ''|A-xI| | + | {{Definición|Nombre=Polinomio característico|imagen=MatrizCuadradaOrdenN.gif|concepto=[[Polinomio]] de grado ''N'' derivado de ''|A-xI<sub>N</sub>|'' donde ''A'' es una [[matriz asociada]] a una transformación lineal ''T''.}} |
| − | |||
| − | |||
| − | Las raíces reales de dicho polinomio mismo serán [[valores propios]] de ''T''. | + | '''Polinomio característico'''. Dícese del [[polinomio]] de grado ''N'' resultante de la ecuación ''|A-xI<sub>N</sub>|'' donde ''A'' es la [[matriz cuadrada]] asociada a la [[aplicación lineal]] ''T'' del mismo orden. |
| + | |||
| + | Las raíces reales de dicho polinomio mismo serán [[Valor propio|valores propios]] de ''T''. | ||
De ahí que los polinomios característico sean medulares para la obtención de los valores, subespacios y vectores propios de una aplicación lineal. También con ellos se verifica la existencia de dichos valores lineales y de la diagonalizabilidad de la matriz. | De ahí que los polinomios característico sean medulares para la obtención de los valores, subespacios y vectores propios de una aplicación lineal. También con ellos se verifica la existencia de dichos valores lineales y de la diagonalizabilidad de la matriz. | ||
| Línea 10: | Línea 10: | ||
Sea ''T'' una aplicación o transformación lineal [[endomorfismo|endomórfica]] de orden ''N'' sobre ''K<sup>N</sup>'' se llama '''polinomio característico''' al resultante de la expresión: | Sea ''T'' una aplicación o transformación lineal [[endomorfismo|endomórfica]] de orden ''N'' sobre ''K<sup>N</sup>'' se llama '''polinomio característico''' al resultante de la expresión: | ||
| − | * ''|A-xI| | + | * ''P(x)=|A-xI<sub>N</sub>|'' |
| − | donde ''A'' es la matriz cuadrada asociada a ''T'', ''I'' es la [[matriz identidad]] de orden ''N''. | + | donde ''A'' es la matriz cuadrada asociada a ''T'', ''I<sub>N</sub>'' es la [[matriz identidad]] de orden ''N''. |
| − | Mientras se conoce como '''ecuación característica''' a ''(A-xI)=0''. | + | Mientras se conoce como '''ecuación característica''' a la expresión del álgebra matricial ''(A-xI<sub>N</sub>)=0''. |
==Propiedades== | ==Propiedades== | ||
Sea un polinomio característico ''P(x)'' de la aplicación lineal ''T'' sobre ''K<sup>N</sup>'', para el mismo se verifican las siguientes propiedades: | Sea un polinomio característico ''P(x)'' de la aplicación lineal ''T'' sobre ''K<sup>N</sup>'', para el mismo se verifican las siguientes propiedades: | ||
| − | # Los valores propios de ''T'' son | + | # Los valores propios de ''T'' son raíces de ''P(x)=0''. |
# Si todas las ''N'' raíces de ''P(x)'' pertecen a ''K'' entonces son valores propios de ''T'' y ésta es diagonalizable. | # Si todas las ''N'' raíces de ''P(x)'' pertecen a ''K'' entonces son valores propios de ''T'' y ésta es diagonalizable. | ||
# Dos matrices semejantes tienen el mismo polinomio característico. | # Dos matrices semejantes tienen el mismo polinomio característico. | ||
| − | |||
==Ejemplos== | ==Ejemplos== | ||
| Línea 63: | Línea 62: | ||
Que como es sabido no tiene solución real. | Que como es sabido no tiene solución real. | ||
| − | En cambio, si ''M'' se definiera sobre [[número complejo|números complejos]]; las soluciones ''i'' y ''-i'' serán valores propios. | + | En cambio, si ''M'' se definiera sobre [[número complejo|números complejos]]; las soluciones ''i'' y ''-i'' serán valores propios de ''M<sub>2</sub>(R)''. |
==Importancia== | ==Importancia== | ||
| Línea 75: | Línea 74: | ||
* [[Matriz cuadrada]] | * [[Matriz cuadrada]] | ||
* [[Matriz identidad]] | * [[Matriz identidad]] | ||
| − | * [[ | + | * [[Matriz diagonal]] |
* [[Determinante]] | * [[Determinante]] | ||
* [[Teorema de Cayley-Hamilton]] | * [[Teorema de Cayley-Hamilton]] | ||
| Línea 81: | Línea 80: | ||
==Fuentes== | ==Fuentes== | ||
* Colectivo de Autores. [[Álgebra lineal]]. [[Editorial Félix Valera]]. [[La Habana]], [[2003]]. | * Colectivo de Autores. [[Álgebra lineal]]. [[Editorial Félix Valera]]. [[La Habana]], [[2003]]. | ||
| − | * | + | * V. V. Voevodin. ''Álgebra lineal'', Editorial Mir Moscú - 1982 |
* Proskuriakov, I. Problemas de Álgebra Lineal. Editorial Mir, Moscú. [[1986]]. | * Proskuriakov, I. Problemas de Álgebra Lineal. Editorial Mir, Moscú. [[1986]]. | ||
* [https://es.wikipedia.org/wiki/Polinomio_característico Polinomio característico en Wikipedia]. Consultado el [[15 de febrero]] de [[2018]]. | * [https://es.wikipedia.org/wiki/Polinomio_característico Polinomio característico en Wikipedia]. Consultado el [[15 de febrero]] de [[2018]]. | ||
última versión al 01:06 5 sep 2019
| ||||||
Polinomio característico. Dícese del polinomio de grado N resultante de la ecuación |A-xIN| donde A es la matriz cuadrada asociada a la aplicación lineal T del mismo orden.
Las raíces reales de dicho polinomio mismo serán valores propios de T.
De ahí que los polinomios característico sean medulares para la obtención de los valores, subespacios y vectores propios de una aplicación lineal. También con ellos se verifica la existencia de dichos valores lineales y de la diagonalizabilidad de la matriz.
Definición
Sea T una aplicación o transformación lineal endomórfica de orden N sobre KN se llama polinomio característico al resultante de la expresión:
- P(x)=|A-xIN|
donde A es la matriz cuadrada asociada a T, IN es la matriz identidad de orden N.
Mientras se conoce como ecuación característica a la expresión del álgebra matricial (A-xIN)=0.
Propiedades
Sea un polinomio característico P(x) de la aplicación lineal T sobre KN, para el mismo se verifican las siguientes propiedades:
- Los valores propios de T son raíces de P(x)=0.
- Si todas las N raíces de P(x) pertecen a K entonces son valores propios de T y ésta es diagonalizable.
- Dos matrices semejantes tienen el mismo polinomio característico.
Ejemplos
Sea la matriz A sobre el conjunto de los reales:
asociada a la aplicación lineal T:R3->R3; obtener los valores propios de A.
1ro. Se plantea |A-kI|=0 para obtener el polinomio característico:
que es reducido a:
- -k3+6k2+2k-12=0 (Polinomio característico de A)
2do. Se determinan las raíces del polinomio:
- -k3+2k+6k2-12=0
- =-k(k2-2)+6(k2-2)
- (6-k)(k2-2)=0
siendo 6 y ![]() que son valores propios de A por ser todos reales.
que son valores propios de A por ser todos reales.
En el caso de la matriz M2(R):
Para determinar si tiene valores propios primero se busca el polinomio característico mediante:
Quedando:
- P(x)=x2+1=0
Que como es sabido no tiene solución real.
En cambio, si M se definiera sobre números complejos; las soluciones i y -i serán valores propios de M2(R).
Importancia
Los valores y vectores propios son clave para la diagonalización de matrices cuadradas, proceso que se hace mediante la resolución del polinomio característico de la matriz cuadrada asociada a la transformación lineal en cuestión, usando por lo general el teorema de Cayley-Hamilton. Para matrices superiores al orden 3, se obtendrán polinomios que no tendrán un método general de factorización.
En todo, caso el polinomio característico permite vincular la búsqueda de valores propios de una aplicación lineal con la resolución de un polinomio de una variable de grado igual al orden de la aplicación, con los inconvenientes y ventajas de esta parte del álgebra.
Véase también
- Vector propio
- Valor propio
- Matriz cuadrada
- Matriz identidad
- Matriz diagonal
- Determinante
- Teorema de Cayley-Hamilton
Fuentes
- Colectivo de Autores. Álgebra lineal. Editorial Félix Valera. La Habana, 2003.
- V. V. Voevodin. Álgebra lineal, Editorial Mir Moscú - 1982
- Proskuriakov, I. Problemas de Álgebra Lineal. Editorial Mir, Moscú. 1986.
- Polinomio característico en Wikipedia. Consultado el 15 de febrero de 2018.